Системой сходящихся сил называют группу двух, трех и более сил, приложенных к телу, линии действия которых пересекаются в некоторой точке.

Пусть, к абсолютно твердому телу приложена система N сил (F₁, F₂, … F_N), расположенных в пространстве так, что их линии действия пересекаются в одной точке О (рисунок 1).

Такую систему сил называют системой сходящихся сил. Упростим систему сходящихся сил, т.е. решим первую задачу статики.

Приведение к равнодействующей

Докажем, что данная система сил эквивалентна одной силе, т.е. приводится к равнодействующей силе.

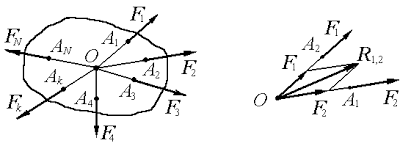
В самом деле, так как сила есть вектор скользящий, то все силы данной системы можно перенести вдоль линий их действия в точку О.

Далее, по четвертой аксиоме, силы F₁ и F₂ можно заменить их равнодействующей R_1,2 (рисунок 1), которая определяется диагональю параллелограмма, построенного на этих силах как на сторонах, и направленной по этой диагонали, т.е.

где R_1,2=F₁+F₂.

Далее можно записать аналогичные соотношения для полученной равнодействующей силы R^*_1,2 и силы F₃, тогда

где R_1,2,3=F₁+F₂+F₃ и т.д.

Для системы N сил окончательно будем иметь

На рисунке 2, a показано построение равнодействующей указанным способом на примере системы, состоящей из четырех сил. Однако процесс определения равнодействующей удобнее вести иным путем, с помощью построения так называемого силового многоугольника.

Силовой многоугольник

Из конца вектора силы F₁ (точки В) проводим вектор ВС, геометрически равный силе F₂. Из конца этого вектора (точки С) проводим вектор СD равный силе F₃. Из конца этого вектора (точки D) проводим вектор DE, равный силе F₄.

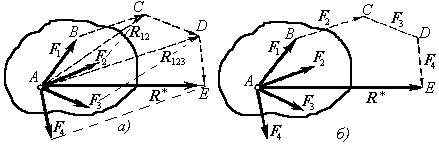
Рисунок 2

Полученный многоугольник ABCDE называется силовым многоугольником. Процесс его построения хорошо виден на рисунке 2, б. Стороны силового многоугольника называются составляющими силами.

Вектор АЕ, соединяющий начало А первой силы с концом Е последней силы и направленный навстречу составляющим силам, называется замыкающей стороной силового многоугольника.

Следовательно, равнодействующая системы сходящихся сил изображается в выбранном масштабе замыкающей силового многоугольника, построенного на составляющих силах.

Нахождение равнодействующей системы сходящихся сил по правилу силового многоугольника называется векторным или геометрическим сложением сил.

Таким образом, мы доказали, что система сходящихся сил в общем случае эквивалентна одной силе, т.е. равнодействующей, которая приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.

Вычисление равнодействующей

Для аналитического определения равнодействующей найдем ее проекции R_x, R_y, R_z на оси декартовой системы координат. Имеем

Тогда величина равнодействующей определится следующей формулой:

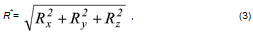
или

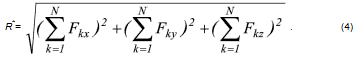
Для определения направления равнодействующей R* воспользуемся обычными выражениями для направляющих косинусов:

Здесь  α ,  β ,  γ — углы между положительным направлением осей координат и равнодействующей.

Равенства (2)-(5) позволяют определить модуль и направление равнодействующей по заданным проекциям составляющих сил.

В случае плоской системы сходящихся сил оси координат можно взять в плоскости действия сил и тогда формулы (2)-(5) упрощаются.

Пример решения задачи по теме
Условия равновесия системы сходящихся сил