В теории сложного движения точек и твердых тел принято считать, что движение точки относительно основной или неподвижной системы отсчета состоит из двух или нескольких более простых движений. Для этого, вводят в рассмотрение вторую (а при необходимости и последующие) подвижную систему отсчета.

Сложным, называют движение точки или твердого тела, рассматриваемое одновременно в неподвижной и подвижной системах отсчета.

Основные понятия и определения

При решении многих инженерных задач приходится рассматривать движение точки по отношению к некоторому твердому телу, которое в свою очередь тоже движется.

При математическом описании такого сложного движения вводится неподвижная система отсчета и система отсчета жестко связанная с движущимся твердым телом, т.е. подвижная система отсчета. Тогда движение точки относительно подвижной системы отсчета называется относительным движением.

Движение твердого тела и неизменно связанной с ним подвижной системы отсчета относительно неподвижной системы называется переносным движением, а движение точки относительно неподвижной системы – абсолютным движением.

Соответственно вводятся понятия абсолютной скорости и абсолютного ускорения V_a, a_a, относительной скорости и относительного ускорения V_r, a_r. Понятия переносной скорости и переносного ускорения V_e, a_e требуют уточнения.

Переносной скоростью и переносным ускорением называются скорость и ускорение той точки твердого тела или подвижной системы отсчета, в которой в данный момент находится движущаяся точка.

Пример сложного движения

Рассмотрим пример, показанный на рисунке 1. Диск вращается вокруг оси, проходящей через центр диска перпендикулярно к его плоскости, с угловой скоростью ω. Введем подвижную систему отсчета xOy, которая вращается вместе с диском.

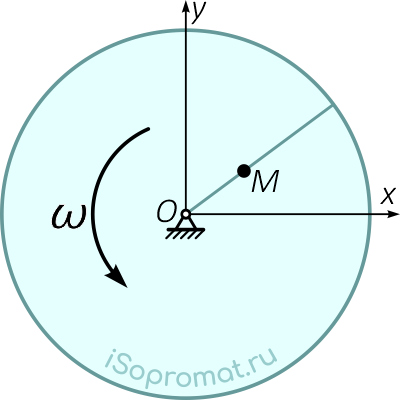
Рисунок 1

По радиусу диска движется точка M по закону OM = s(t).

Таким образом, точка M участвует одновременно в двух движениях — движется относительно диска по радиусу (относительное движение) и, вместе с диском, вращается вокруг оси, проходящей через центр диска (переносное движение).

Относительной скоростью и относительным ускорением точки M будет являться скорость и ускорение в движении вдоль радиуса диска.

Переносной скоростью и переносным ускорением будет являться скорость и ускорение той точки диска, в которой в данный момент находится точка M.

Далее: