Условие равновесия пространственной системы сходящихся сил гласит: необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую из трех координатных осей равнялись нулю.

Пусть на свободное твердое тело действует система сходящихся сил (F₁,  F₂, … F_N). Сложив по правилу силового многоугольника N-1 этих сил, приведем данную систему сходящихся сил к системе двух сил (R₁, F_N).

Но, по первой аксиоме, две силы R₁ и F_N приложенные к твердому телу, эквивалентны нулю, т.е. находятся в равновесии только в том случае, когда они имеют равные модули и направлены по одной прямой в противоположные стороны, т.е. если их равнодействующая R^*= R₁ + F_N равна нулю.

Следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этой системы сил равнялась нулю, т.е.

Это векторное условие равновесия системы сходящихся сил.

Так как равнодействующая R* изображается вектором, замыкающим силовой многоугольник, то геометрически условие равновесия системы сходящихся сил означает, что силовой многоугольник, построенный на векторах слагаемых сил данной системы, замкнут.

Выразим теперь это условие аналитически. Из предыдущего параграфа известно, что модуль равнодействующей системы сходящихся сил определяется по формуле

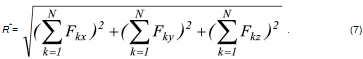
Но при равновесии R*= 0, а следовательно равно нулю и подкоренное выражение формулы (2). Поскольку под знаком корня стоит сумма положительных чисел, то R* может равняться нулю только в случае, если каждое из этих слагаемых равно нулю в отдельности, т.е.

Таким образом, для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую из трех выбранных любым образом координатных осей равнялись нулю.

Имея плоскую систему сходящихся сил, всегда можно плоскость, в которой расположены силы, принять за координатную плоскость хОу. Тогда третье условие в формулах (8) выполняется тождественно, и условия равновесия, в рассматриваемом случае, сведутся к двум следующим условиям:

Т.е., для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую из двух выбранных любым образом координатных осей, лежащих в плоскости действия сил данной системы, равнялись нулю.

Примеры решения задач >
Равновесие пространственной системы сходящихся сил >