Для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая системы равнялась нулю, т. е. чтобы силовой многоугольник был замкнут.
Определение равнодействующей
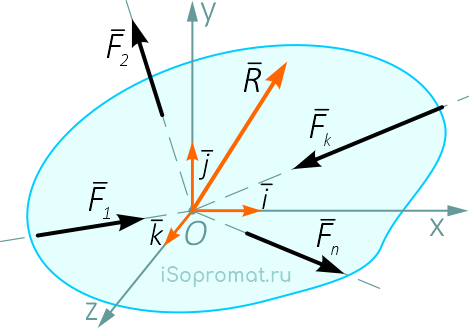
Равнодействующая пространственной системы сходящихся сил R приложена в точке пересечения линий действия слагаемых сил и является замыкающей стороной силового многоугольника, построенного на этих силах, т. е.
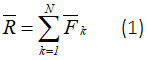
В отличие от соответствующей плоской задачи силовой многоугольник не является плоским, т.е. он представляет собой ломаную пространственную линию.
Проекции равнодействующей силы R на оси декартовых координат х, у, z равны суммам проекций слагаемых сил па соответствующие оси, т. е.
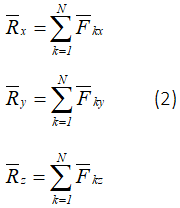
Модуль равнодействующей R равен
![]()
направляющие косинусы определяются по формулам:
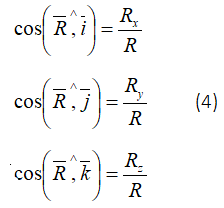
Уравнения равновесия
Для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая равнялась нулю: R=0, т. е. чтобы силовой многоугольник был замкнут. При этом уравнения равновесия имеют вид
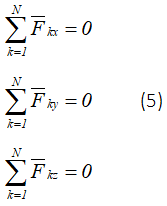
Задача является статически определенной, если число алгебраических неизвестных не более трех (предполагается, что все силы не лежат на одной прямой или в одной плоскости).
Так, если известны направления всех сил, то можно определить модули трех сил.
Далее: