Вращением твердого тела вокруг неподвижной оси называют движение, при котором хотя бы две точки тела на протяжении всего времени остаются неподвижными.
Прямая, проходящая через эти точки, называется осью вращения.
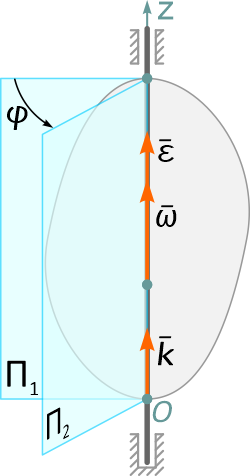
Вращательное движение твердого тела определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения.
Одна из этих плоскостей неподвижна, вторая скреплена с твердым телом и поворачивается вместе с ним (рисунок 2.3).
Изменение этого угла с течением времени и есть закон вращательного движения:
![]()
Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения (ось Oz на рисунке 2.3). Угол измеряется в радианах.
Определение кинематических параметров вращающегося твердого тела
Быстрота изменения угла φ – это угловая скорость вращения твердого тела:
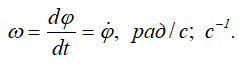
Приняв k как единичный орт положительного направления оси, получим вектор угловой скорости
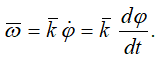
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны (разнонаправлены).
Изменение угловой скорости характеризуется угловым ускорением:
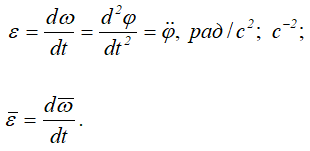
Вектор углового ускорения, как и вектор угловой скорости, направлен по оси вращения.
При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Для некоторых частных случаев вращательного движения могут быть использованы формулы:
- равномерное вращение (ω — const)
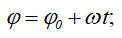
- равнопеременное вращение (ε — const)
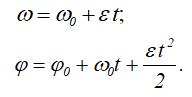
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. При этом, один оборот – это 2π радиан:
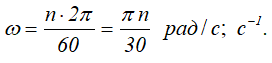
Далее: