Лабораторная работа № 4. Определение величины коэффициента поперечной деформации для стали.
Цель работы – экспериментально определить величину коэффициента поперечной деформации (коэффициента Пуассона) для стали при испытании на растяжение.
Основные сведения
Под действием осевой нагрузки стержень изменяет свою длину и размеры поперечного сечения. Соотношение между величинами поперечной и продольной деформации для каждого материала при растяжении или сжатии является постоянной величиной и характеризует упругие свойства материала.
Абсолютную величину отношения поперечной деформации εпоп стержня к продольной деформации εпр называют коэффициентом Пуассона:
Его можно вычислить, если измерить изменения линейных размеров стержня в поперечном и продольном направлениях при действии осевой нагрузки, вызывающей только упругие деформации.
В данной работе определение коэффициента Пуассона проводится на образце, растягиваемом на испытательной машине Р-5. Образец для испытаний представляет собой широкую полосу, дающую возможность установки тензодатчиков в поперечном направлении; его длина в 4-5 раза больше ширины для исключения влияния неравномерности распределения деформаций в местах приложения нагрузки к образцу.
Наиболее быстро и наглядно коэффициент Пуассона определяется при помощи тензодатчиков сопротивления. Принцип работы датчика основан на изменении его омического сопротивления вследствие деформации проволоки датчика.
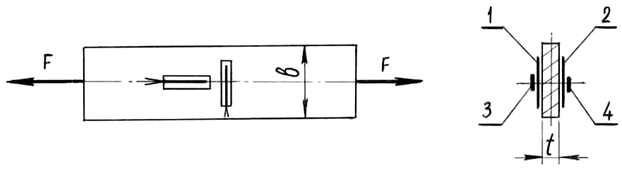
Рис. 4.1. Схема расположения рабочих тензодатчиков на образце
Рабочие датчики наклеиваются на испытуемый образец в поперечном (датчики 1,2) и в продольном (датчики 3,4) направлениях попарно на обеих сторонах растягиваемой пластины с целью исключения влияния возможного эксцентриситета продольного усилия.
Изменения сопротивления рабочих датчиков, вызванные деформацией образца, фиксируются измерительным прибором ИДЦ-1.
Порядок выполнения и обработка результатов
После установки и закрепления испытуемого образца производим его начальное нагружение небольшой нагрузкой для обжатия образца в захватах машины. Показания тензодатчиков при этой нагрузке записывают в таблицу как начало отсчета. Чем больше деформации, тем точнее можно их измерить, поэтому после предварительного обжатия нагрузку доводим до максимального значения.
При проведении опыта нужно избегать мертвых ходов приборов, для этого изменение нагрузки следует производить только в направлении, соответствующем возрастанию нагрузки. Снимаем показания тензодатчиков, также записав их значения в таблицу. После проведения опыта следует проверить начальные отчеты.
Определяем приращение показаний каждого тензодатчика, затем – средние значения приращений показаний для датчиков, установленных в продольном ΔПпр и поперечном ΔПпоп направлениях, и экспериментальное значение коэффициента Пуассона. При испытании на растяжение продольные тензодатчики показывают увеличение отсчетов, поперечные — их уменьшение.
Так как сигналы от всех тензодатчиков идут на один и тот же регистрирующий прибор, то цена деления шкалы прибора не играет роли, и коэффициент Пуассона следует вычислять по формуле
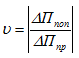
Полученный результат необходимо сопоставить с известными значениями коэффициента Пуассона из справочника или учебной литературы и сделать заключение о достоверности проведенного эксперимента.
Контрольные вопросы
- Какая величина называется коэффициентом поперечной деформации?
- Как экспериментально определить коэффициент поперечной деформации (коэффициент Пуассона)?
- Почему при определении продольных и поперечных деформаций используют по два тензометра?
Испытание материалов на кручение >
Другие лабораторные работы >
Примеры решения задач >
