Коэффициент Пуассона (коэффициент поперечной деформации) — одна из механических характеристик материалов, показывает зависимость между продольными и поперечными деформациями при линейном нагружении элемента, характеризует упругие свойства материала.

Обозначается строчными греческими буквами ν (ню) или μ (мю) и не имеет размерности.

Коэффициент Пуассона определяется отношением относительных поперечных ε_поп и продольных ε_пр деформаций бруса (элемента):

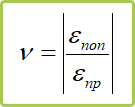
Определение коэффициента поперечной деформации

Рассмотрим деформацию элемента цилиндрической формы (рис. 1) который до нагружения имеет следующие начальные размеры:

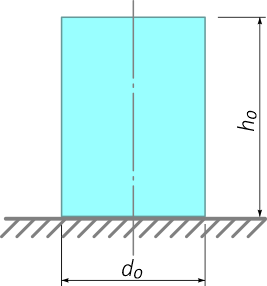
Рис. 1. Размеры бруса до нагружения

здесь
h₀ — начальный продольный размер (длина или высота);
d₀ — начальный поперечный размер (диаметр или ширина).

После нагружения некоторой продольной силой (например, сжимающей) брус изменит свои размеры: продольный размер уменьшится, а поперечный — увеличится (рис. 2)

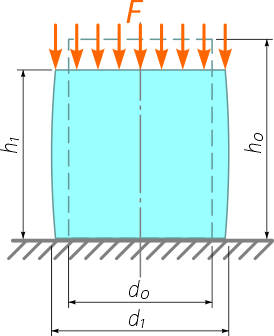
Рис. 2. Размеры бруса после деформации

Полученные в результате деформации размеры обозначим соответственно h₁ и d₁.

Абсолютные продольные Δh и поперечные Δd деформации бруса

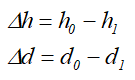
Отношение абсолютных деформаций к соответствующим начальным размерам определяет относительные деформации:

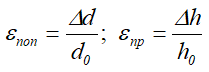
а их отношение в свою очередь определяет коэффициент Пуассона материала бруса.

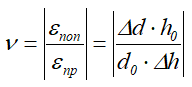
Значение коэффициента принимается по модулю, т.к. продольная и поперечная деформации всегда имеют противоположные знаки (удлинение бруса приводит к его сужению и наоборот).

Значения коэффициента Пуассона для материалов определяется в ходе испытаний по определению коэффициента поперечной деформации.

В таблице 1 приведены сравнительные значения коэффициента для некоторых материалов.

Таблица 1. Значения коэффициента Пуассона для различных материалов

Материал	Коэффициент Пуассона
Сталь	0,3
Чугун	0,25
Медь	0,32
Титан	0,3
Алюминий	0,3
Бетон	0,16
Резина	0,5

Для всех существующих материалов значение коэффициента поперечной деформации находится в пределах от 0 (пробковое дерево) до 0,5 (резина).

Минимальные значения коэффициента свойственны хрупким материалам, максимальные — пластичным.

Для сталей, в зависимости от марки, коэффициент Пуассона принимает значения от 0,27 до 0,32.

---

Дополнительно: