Пример решения задачи по расчету координат положения центра тяжести (центра масс) сложного сечения методом разбиения на простые фигуры.
Задача
Определить координаты центра тяжести сложного сечения.

Пример решения
Подробный пример определения координат центра тяжести сложного плоского сечения в нашем коротком видео:
Разбиваем заданную фигуру на простые, для которых легко можно рассчитать площадь и положение центра тяжести:
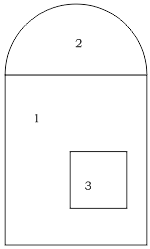
В данном случае это:
1 — прямоугольник;
2 — полукруг;
3 — квадрат.
Площадь всей фигуры составляет:
Задаем систему координат, и показываем центры тяжести каждой из простых фигур:
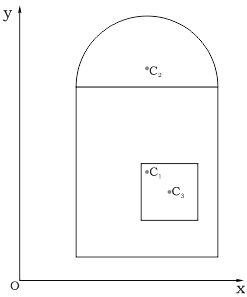
Определив расстояние от осей x и y до соответствующих центров тяжести элементарных фигур:
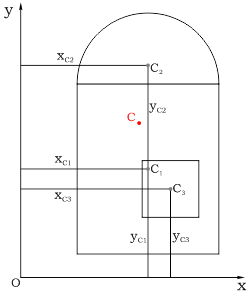
Рассчитываем положение центра тяжести C всей фигуры сложного сечения:
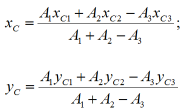
Далее: