Пример решения задачи по расчету минимального диаметра стального стержня обеспечивающего его прочность.
Задача
Подобрать по условию прочности диаметр стального стержня нагруженного продольной растягивающей силой F=10кН. Допустимые напряжения σ=160МПа.
Другие примеры решений >
Помощь с решением задач >
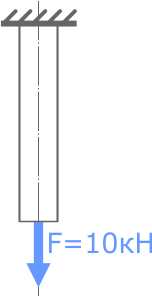
Решение
Для того чтобы стержень был прочным, нормальные напряжения σ в его поперечных сечениях не должны превышать заданных допустимых значений.
Условие прочности при продольном нагружении
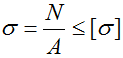
где A — площадь поперечного сечения,
N – величина внутренней продольной силы, которая была определена ранее (N=10кН).
От диаметра, который мы будем рассчитывать, в данном выражении зависит только площадь A, поэтому получаем:
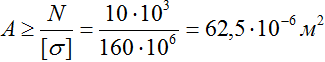
В квадратных миллиметрах площадь сечения представить проще:
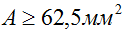
То есть для того чтобы стержень был прочным, площадь его поперечного сечения независимо от формы должна быть не менее указанной величины.
Из формулы площади круга выражаем его расчетный диаметр
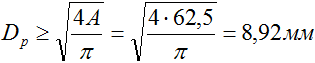
Это минимальный диаметр стержня, обеспечивающий его прочность.
Если в задании нет дополнительных условий, полученный размер можно округлить до целого миллиметра, но только в большую сторону.
Окончательно принимаем D=9мм.