Модуль Юнга (также: модуль упругости Ⅰ рода, модуль продольной упругости) – механическая характеристика материалов, определяющая их способность сопротивляться продольным деформациям.

Физический смысл: показывает степень жесткости материала.

Назван в честь английского ученого Томаса Юнга.

Обозначается латинской прописной буквой E
Единица измерения – Паскаль [Па].

В сопротивлении материалов модуль продольной упругости используется в расчетах на жесткость при растяжении-сжатии и изгибе, а также в расчетах сжатых стержней на устойчивость.

Учитывая то, что практически все конструкционные материалы имеют значение E высокого порядка (как правило, 10⁹ Па), его размерность часто записывают с помощью кратной приставки «гига» (гигапаскаль [ГПа]=10⁹Па)

Для всех материалов величину модуля Юнга можно определить в ходе эксперимента по определению модуля упругости Ⅰ рода.

Определение модуля упругости

Для стали, приближенное значение модуля продольной упругости можно определить по диаграмме напряжений получаемой при испытаниях на растяжение.

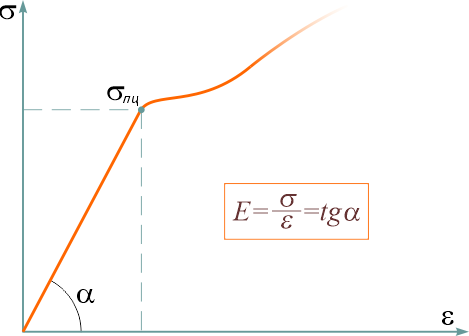
В этом случае модуль Юнга равен отношению нормальных напряжений к соответствующим относительным деформациям, на участке диаграммы (рис. 1) до предела пропорциональности σ_пц (тангенсу угла α наклона участка пропорциональности к оси деформаций ε).

В таблице 1 приведены сравнительные значения модуля Юнга для некоторых, наиболее часто используемых материалов.

Таблица 1. Значения модуля Юнга для различных материалов

Материал	Модуль Юнга E, [ГПа]
Сталь	200
Чугун	120
Серый чугун	110
Алюминий	70
Дюралюминий	74
Титан	120
Бронза	100
Латунь	95
Медь	110
Олово	35
Хром	300
Никель	210
Кремний	110
Свинец	18
Бетон	20
Дерево	10
Стекло	70
Резина	0,002

Применение модуля Юнга для расчета деформаций

Модуль упругости Ⅰ рода является коэффициентом пропорциональности в формуле, описывающей закон Гука:

Связка модуля Юнга с геометрическими характеристиками поперечных сечений бруса показывает их жесткость:

EA – жесткость поперечного сечения при растяжении-сжатии,
где A – площадь поперечного сечения стержня;

EI – жесткость поперечного сечения балки при изгибе (изгибная жесткость),
где I – осевой момент инерции сечения балки.

Пример расчета деформации:

Задача

Стальной стержень (модуль Юнга E=200ГПа) растянут силой F=35кН. Площадь поперечного сечения стержня A=1см², длина l=40см.

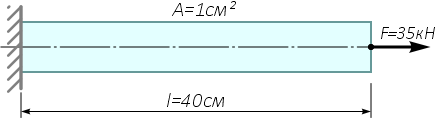
Определим удлинение стержня.

Решение

Для расчета деформации стержня перепишем закон Гука с использованием заданных параметров, откуда выразим и рассчитаем его удлинение

Таким образом, удлинение стержня составило 0,7мм.

Нетрудно заметить, что замена материала стержня на бронзу с модулем Юнга E=100МПа приведет к увеличению деформации в два раза, до 1,4мм.

---

Далее: