Рассмотрим кинематический анализ стержневых систем для определения и оценки их геометрической неизменяемости:
Очевидно, что сооружения должны быть геометрически неизменяемыми, то есть постоянно сохранять геометрическую форму, заданную при возведении.
Цель кинематического анализа — установить является ли система геометрически неизменяемой или геометрически изменяемой.
Геометрически неизменяемой принято называть систему соединенных между собой элементов сооружения, изменение взаимного расположения отдельных частей которого возможно лишь за счет их деформации (рисунок 1.17). Именно такие системы применяются в практике строительства.
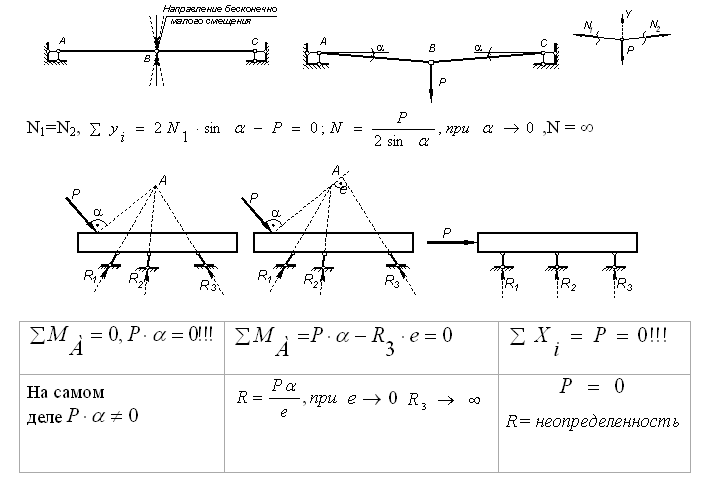
Рис. 1.17 – Геометрически неизменяемая система
Геометрически изменяемыми будем называть системы, в которых возможны взаимные перемещения отдельных элементов без их деформации (рисунок 1.18).
Они представляют собой механизмы и некоторые из них применяются в различных машинах.
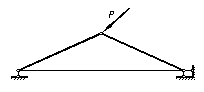
Рис. 1.18 – Геометрически изменяемая система
Геометрическая неизменяемость зависит не только от количества связей в системе, но и от их взаимного расположения.
Системы, в которых возможны малые взаимные перемещения без деформации элементов, называются мгновенно изменяемыми.
После осуществления этих малых перемещении система может стать неизменяемой (рисунок 1.17).
Подобные системы названы так И.М.Рабиновичем.
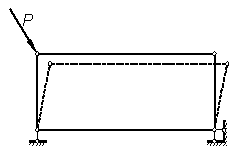
Рис. 1.19 — Примеры мгновенно изменяемых систем с пояснениями причин невозможности их эксплуатации
Определимся с некоторыми категориями кинематического анализа:
— диски — простейшие геометрически неизменяемые элементы систем;
Стержни
Плоские фигуры
Треугольник
Рис. 1.20 — Диски
— количество степеней свободы системы определяется числом независимых геометрических параметров однозначно определяющих ее положение в плоскости (пространстве);

Рис. 1.21- Определение количества степеней степеней свободы
Для того, чтобы превратить системы в неизменяемые (а именно они нас и интересуют) необходимо наложить связи (по количеству степеней свободы).
Поговорим о связях — устройствах, предотвращающих взаимные поступательные движения и повороты:
а) Связь 1 рода – стержень (рисунок 1.22).
Она не позволяет смещаться в направлении связи и таким образом снимает одну степень свободы.
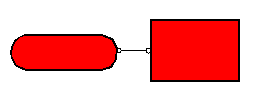
Рис. 1.22 – Связь первого рода
б) Шарнир — препятствует любым взаимным линейным смещениям — снимает в плоскости две степени свободы (соответствует двум непараллельным стержням) (рисунок 1.23).

Рис. 1.23 – Пример шарнирной связи
Шарнир, соединяющий два диска, называется простым.
А если в соединении дисков более двух — кратным.
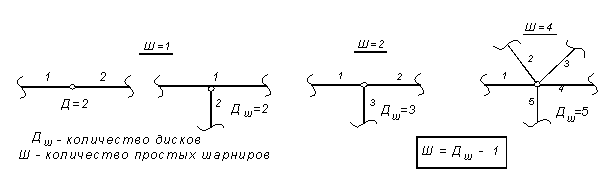
Рис. 1.24 – Определение количества шарниров
в) Припайка — препятствует любым взаимным перемещениям (линейным и повороту).
Соответствует шарниру и стержню, линия действия которого не проходит через шарнир или трем непараллельным или непересекающимся в одной точке стержням (рисунок 1.25).

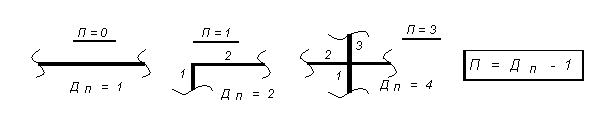
Рис. 1.25 – Определение количества припаек
Далее: