Решение практических работ по технической механике (в том числе задач, расчетно-графических и контрольных работ по теоретической механике и сопротивлению материалов) со всеми расчетами и графическими построениями.

Здесь в каждом задании показаны основные этапы расчетов. Подробные решения со всеми пояснениями можно посмотреть по ссылке, приведенной после каждой задачи.

Помощь с решением

Номера заданий, темы задач и расчетные схемы в разных учебных заведениях могут отличаться.

Определение величины и направления неизвестных реакций в стержневой системе находящейся под действием груза

Практическая работа №1 по теме «Определение величины и направления неизвестных реакций в стержневой системе находящейся под действием груза».

Задание

Определить реакции стержней, удерживающих грузы F₁=1,2кН и F₂=0,8кН.

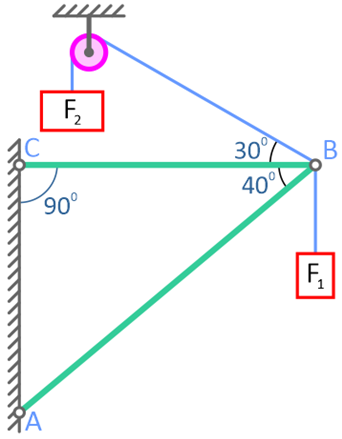
Решение

1. Рассмотрим равновесие шарнира В.

2. Освобождаем соединяющий стержни шарнир B от связей и изображаем действующие на него активные силы и реакции связей.

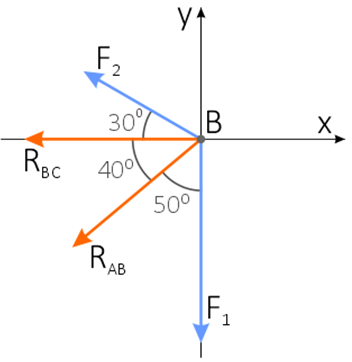
3. Выбираем систему координат x-y и составляем уравнения равновесия для системы сил, действующих на шарнир В.

Сумма проекций всех сил на оси x и y

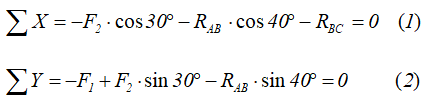
4. Определяем реакции стержней R_AB и R_BC, решая уравнения (1) и (2).

Из уравнения (2)

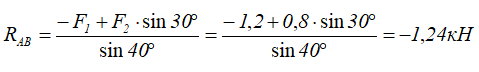
Отрицательное значение указывает на то, что реакцию надо направить в противоположную сторону.

Подставляем найденное значение R_AB в уравнение (1) и получаем

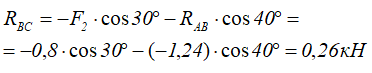
5. Проверяем правильность полученных результатов, решая задачу графически.

Полученная система сил находится в равновесии, следовательно, силовой многоугольник, построенный для этой системы сил, должен быть замкнутым.

Строим силовой многоугольник

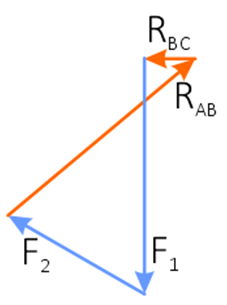
Силовой многоугольник замкнут. Графическое решение подтверждает правильность первого решения.

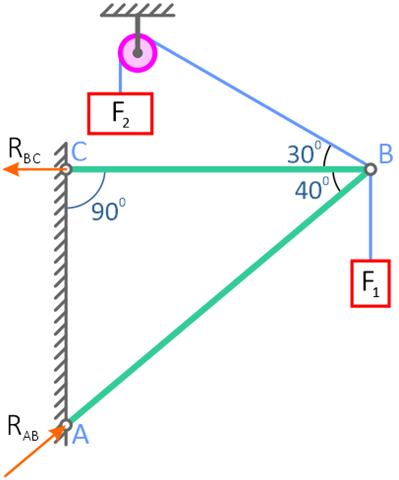
Ответ: реакции стержней, удерживающих грузы R_AB=1,24кН, R_BC=0,26кН

Подробное решение

Определение внутренних усилий в стержнях конструкции аналитическим и графическим способами

Практическая работа №2 по теме «Определение внутренних усилий в стержнях конструкции аналитическим и графическим способами».

Задание

Определить силы в стержнях 1, 2, 3 и 4 заданной фермы, возникающие под действием внешних усилий F₁=15кН и F₂=35кН, аналитическим способом.

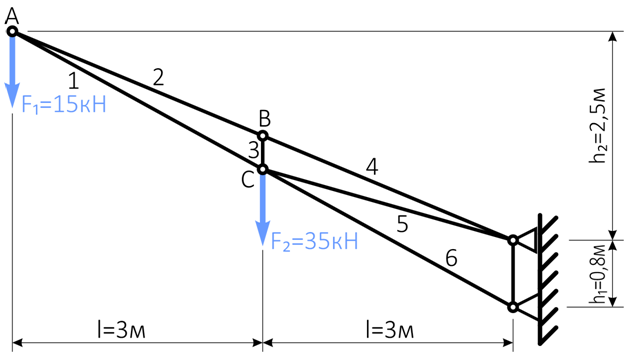
Решение

1. Определение усилий в стержнях 1 и 2

Рассматриваем равновесие узла A.

Показываем действующие на него внешнюю силу и усилия в стержнях.

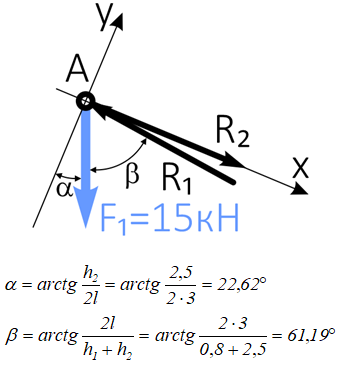
Выбираем систему координат, направив одну из осей вдоль одного из неизвестных усилий.

Cоставляем уравнения равновесия для системы сил, действующих на шарнир A.

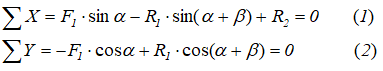
Определяем усилия в стержнях R₁ и R₂, решая совместно уравнения (1) и (2).

Из уравнения (2)

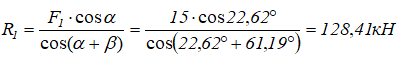
Подставляем найденное значение R₁ в уравнение (1) и получаем

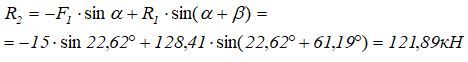
2. Определение усилий в стержнях 3 и 4

Рассматриваем равновесие узла В.

Показываем действующие усилия в стержнях и систему координат

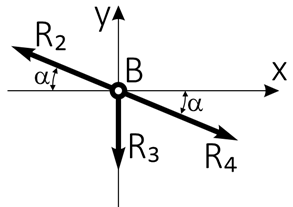
Составляем уравнения равновесия для системы сил, действующих на шарнир В.

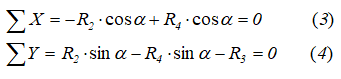
Определяем реакции стержней R₃ и R₄, решая уравнения (3) и (4).

Из уравнения (3)

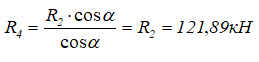
Подставляем найденное значение R₄ в уравнение (4) и получаем

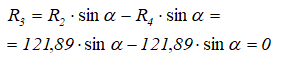
Ответ: R₁=128,41кН, R₂=121,89кН, R₃=0кН, R₄=121,89кН.

Подробное решение

Определение реакций опор двуопорной балки, нагруженной системой внешних сил

Практическая работа №3 по теме «Определение реакций опор двуопорной балки, нагруженной системой внешних сил».

Задание

Определить опорные реакции балки закрепленной на двух шарнирных опорах

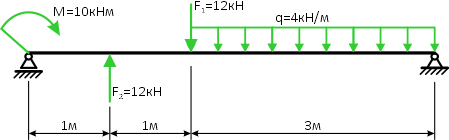
Решение

1. Изобразим балку с действующими на неё нагрузками (рис. а).

2. Изображаем оси координат (рис. б).

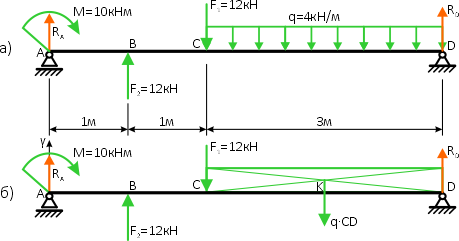
3. Равнодействующая равномерно распределённой нагрузки, приложенная в точке пересечения диагоналей прямоугольника (рис. б), переносится по линии своего действия в середину участка CD, в точку К.

4. Освобождаем балку от опор, заменив их опорными реакциями (рис. б).

5. Составляем уравнения равновесия статики и определяем неизвестные реакции опор.

Для плоской системы параллельных сил достаточно двух уравнений равновесия.

Составим уравнения равновесия балки, записав сумму моментов нагрузок относительно точек расположенных на опорах. При этом все нагрузки, стремящиеся повернуть балку относительно точки опоры в одну сторону, записываются с одинаковыми знаками.

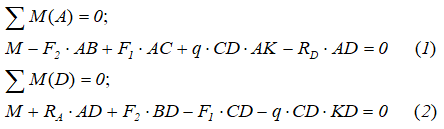
Из уравнений (1) и (2) определяем:

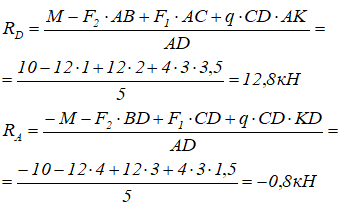
значение реакции R_A получено со знаком минус. Это означает, что она будет направлена вертикально вниз.

6. Проверяем правильность найденных опорных реакций балки, составив уравнение суммы проекций всех сил на вертикальную ось Y.

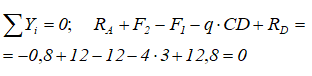
Условие равновесия балки ΣУ_i=0 выполняется, следовательно, опорные реакции определены верно.

Ответ: R_A=-0,8кН; R_D=12,8кН.

Подробное решение

Определение опорных реакций в жесткой заделке консольной балки

Практическая работа №4 по теме «Определение опорных реакций в жесткой заделке консольной балки».

Задание

Определить реакции опор в жестком защемлении консольной балки

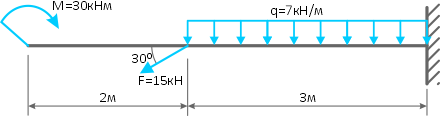
Решение

В целом эта задача решается аналогично предыдущей, с тем отличием, что здесь в защемлении появляется реакция момент и сила F, расположенная под углом к балке, будет давать горизонтальную составляющую реакции в заделке.

Задаем направление реакций в защемлении

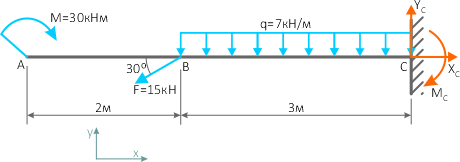
и составляем три уравнения равновесия балки

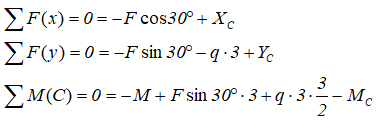
Откуда находим величину искомых реакций

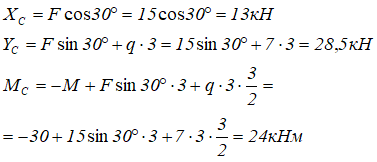
Все значения реакций получились положительными, а это значит, что их направление было задано верно.

При необходимости, можно так же выполнить проверку вычислений составив уравнение суммы моментов относительно точки A или B, которая должна быть равна нулю.

Ответ: X_C=13кН; Y_C=28,5кН; M_C=24кНм.

Подробное решение

Определение центра тяжести сложной фигуры

Практическая работа №5 по теме «Определение центра тяжести сложной фигуры».

Задание

Определить координаты центра тяжести заданного сечения сложной формы.

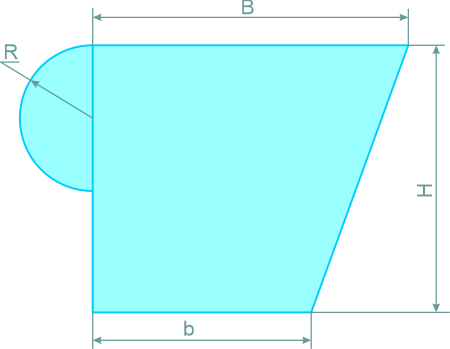
Дано: B=130мм, b=90мм, H=110мм, R=30мм.

Решение

Для решения задачи используем метод разделения на простые части и метод отрицательных площадей.

Подробный пример определения координат центра тяжести сложной фигуры в нашем коротком видео:

Другие видео

Разделим заданное сечение на простые фигуры – полукруг и прямоугольник, из которого вычтем прямоугольный треугольник.

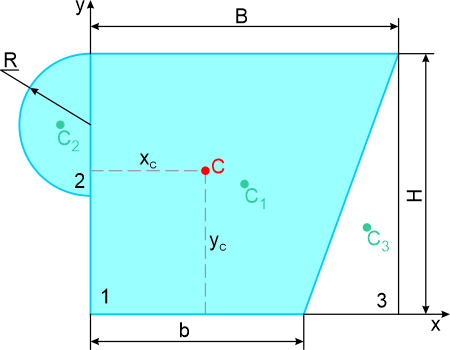
Через нижнюю левую точку фигуры проведем координатные оси x и y.

Рассчитаем необходимые для решения задачи площади A и координаты x,y центров тяжести C_i отдельных простых фигур:

Прямоугольник (1)
Площадь и положение центра тяжести

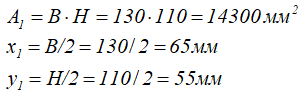
Полукруг (2)
Площадь и положение центра тяжести

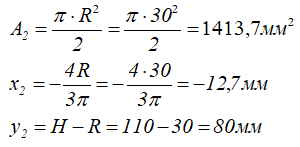
Прямоугольный треугольник (3) (вычитаемая фигура)
Площадь и положение центра тяжести

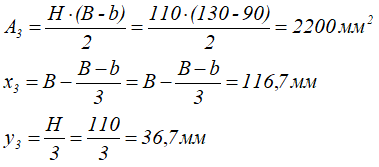
Координаты x и y центра тяжести C всей сложной фигуры определим по формулам

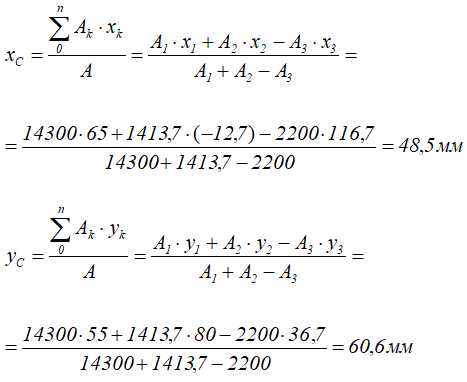
Ответ: Центр тяжести заданного сечения находится в точке с координатами x_C=48,5мм, y_C=60,6мм.

Подробное решение

Определение координат центра тяжести составного сечения из стандартного проката

Практическая работа №6 по теме «Определение координат центра тяжести составного сечения из стандартного проката».

Задание

Определить координаты центра тяжести сечения, составленного из швеллера №16, равнобокого (5,6) и неравнобокого (8/5) уголков и прямой прямоугольной пластины толщиной 10мм.

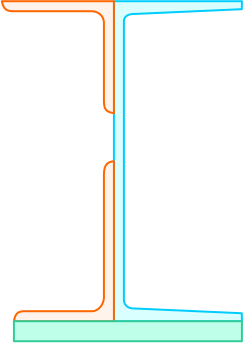
Решение

Из сортаментов прокатной стали выпишем необходимые для решения геометрические характеристики профилей составляющих сечение:

Уголок равнобокий 5,6 (1)
Размеры, положение центра тяжести и площадь

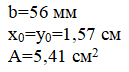
Уголок неравнобокий 8/5 (2)
Размеры, положение центра тяжести и площадь

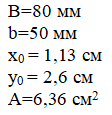
Швеллер №16 (3)
Размеры, положение центра тяжести и площадь

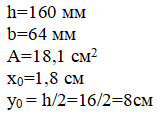
Определим параметры полосы (4)
Размеры, положение центра тяжести и площадь

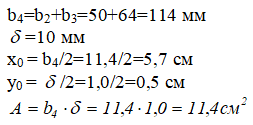
Проведем оси системы координат xOy

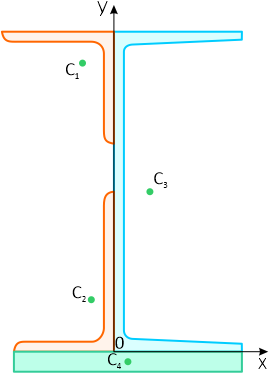
Координаты x и y центра тяжести C всего составного сечения определим по формулам

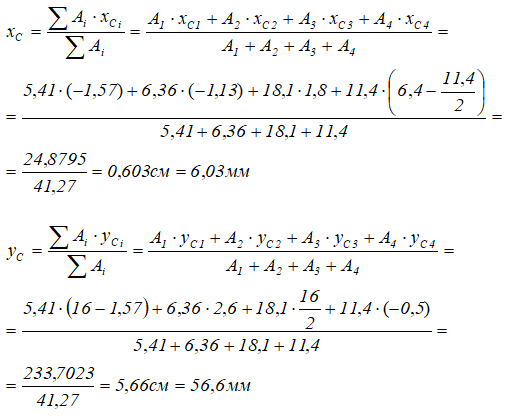
Покажем положение центра тяжести на самом сечении

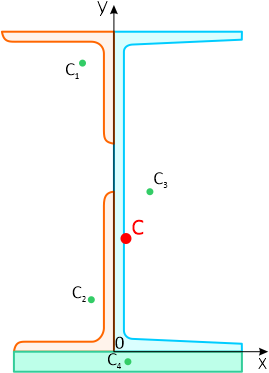
Ответ: Таким образом, центр тяжести заданного составного сечения находится в точке с координатами x_C=6,03мм, y_C=56,6мм.

Подробное решение

Построение эпюр продольных сил и напряжений при растяжении и сжатии стержня

Практическая работа №7 по теме «Построение эпюр продольных сил и напряжений при растяжении и сжатии стержня».

Задание

Для ступенчатого стального бруса требуется:
а) определить значение продольных сил и нормальных напряжений по длине бруса;
б) построить эпюры N и σ;
в) определить абсолютное удлинение (укорочение) бруса.

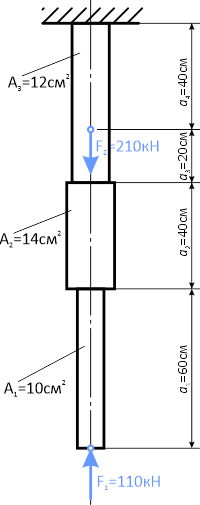
Модуль продольной упругости E=200ГПа.

Решение

Стержень имеет 2 силовых участка.

Рассчитаем величину внутренних продольных сил N по каждому участку стержня методом сечений

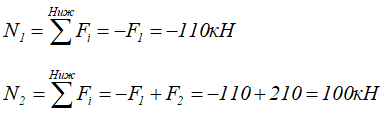
По полученным данным строим эпюру внутренних продольных сил N

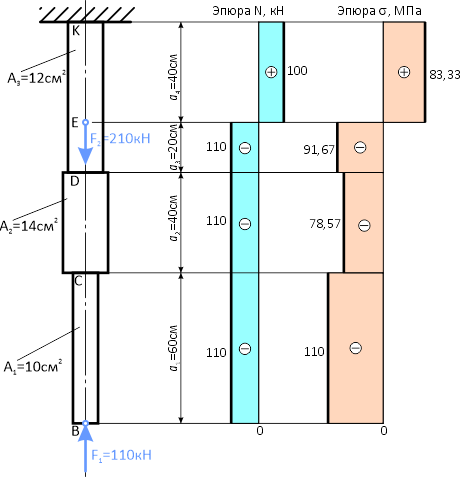
Рассчитаем нормальных напряжений σ по участкам стержня

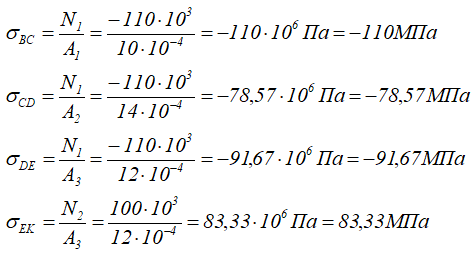
По полученным данным строим эпюру нормальных напряжений

Расчет продольных деформаций участков стержня

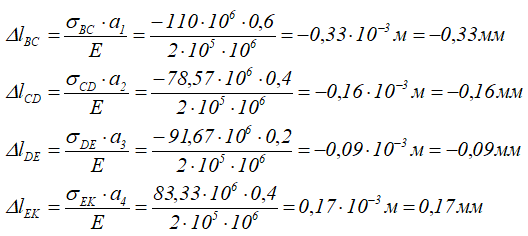
Полное изменение длины стержня определим, сложив с учётом знаков, деформации всех участков стержня

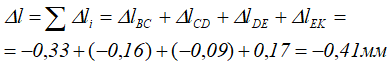
Ответ: Таким образом, абсолютное укорочение бруса равно 0,41мм.

Подробное решение

Построение эпюр крутящих моментов при кручении и подбор диаметра вала по условию прочности и жесткости

Практическая работа №8 по теме «Построение эпюр крутящих моментов при кручении и подбор диаметра вала по условию прочности и жесткости».

Задание

К стальному валу приложены четыре момента.

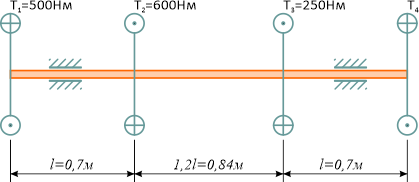
Требуется:

1. Построить эпюру крутящих моментов;
2. При заданном значении [τ]=35МПа определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей величины;
3. Построить эпюру углов закручивания.

Решение

Определим реактивный момент M₄, задав ему произвольное направление.

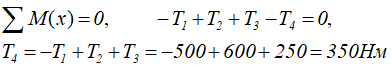
Определим крутящие моменты по участкам вала методом сечений.

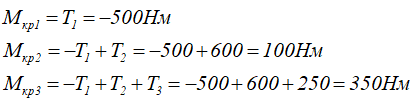
По полученным данным строим эпюру крутящих моментов.

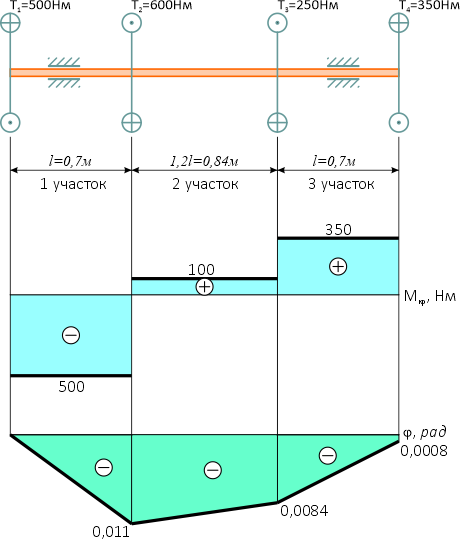
По эпюре видно, что наибольший крутящий момент |M_max|=500Нм.

Из условия прочности определим значение момента сопротивления кручению и диаметр вала:

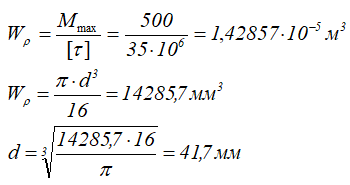
Округляем диаметр до ближайшей большей величины кратной 5.

Принимаем d=45мм.

Построение эпюры углов закручивания

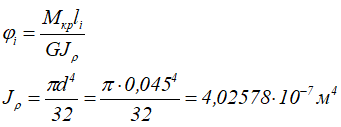
За начало координат примем крайнее левое сечение вала.

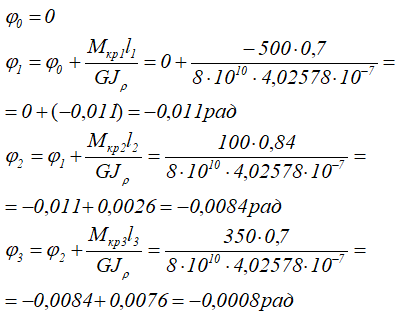
По полученным данным строим эпюру углов закручивания.

Ответ: диаметр вала d=45мм.

Подробное решение

Построение эпюр поперечных сил и изгибающих моментов при изгибе и подбор сечений балки

Практическая работа №9 по теме «Построение эпюр поперечных сил и изгибающих моментов при изгибе и подбор сечений балки».

Задание

Для заданной балки

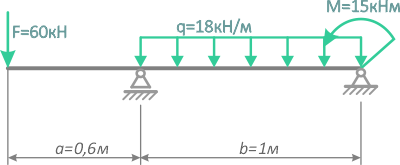
требуется:

1. Построить эпюры изгибающих моментов в M_x и поперечных сил Q_y,
2. Подобрать квадратное сечение балки, если [σ]=120МПа.

Решение

Направим реакции опор вверх и запишем суммы моментов нагрузок приложенных к балке относительно точек на опорах, откуда находим реакции

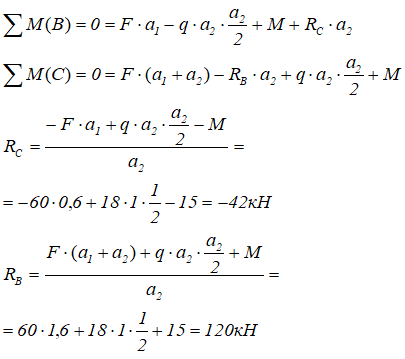
Знак «минус» реакции R_C говорит о том, что она направлена в противоположную сторону (т.е. вниз).

Выполним проверку найденных реакций опор

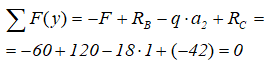
Реакции опор определены верно.

Рассчитаем значения внутренних поперечных сил и изгибающих моментов в сечениях балки на каждом силовом участке методом сечений.

Балка имеет 2 силовых участка.

1 участок (AB) 0≤z₁≤0,6м

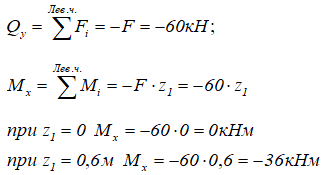
2 участок (BC) 0≤z₂≤1м

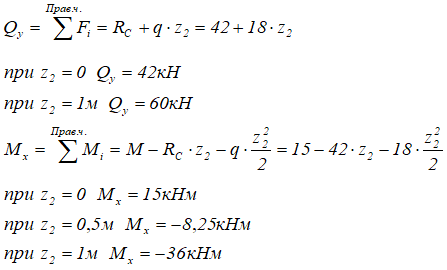
Значения Q_y на границах 2 участка имеют одинаковый знак, поэтому на этом участке, на эпюре M_x экстремума не будет.

По полученным данным строим эпюры внутренних поперечных сил и изгибающих моментов.

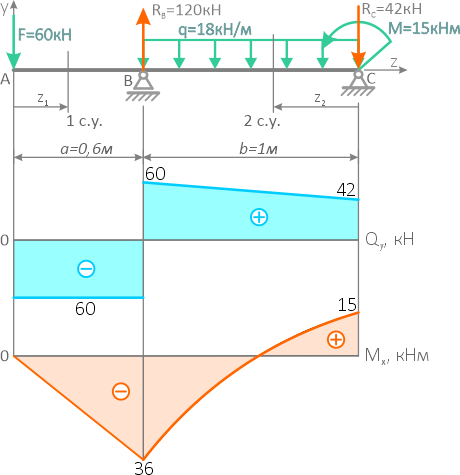
Подбор квадратного сечения балки выполняется по условию прочности по нормальным напряжениям

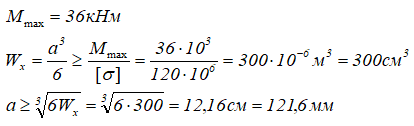
Ответ: Эпюры построены, размер квадратного сечения балки должен быть не менее a=121,6мм.

Подробное решение

Помощь с решением