Пример решения задачи по определению усилий в двух стержнях, скрепленных шарнирно между собой и с вертикальной опорной стеной, в точке соединения которых подвешен груз.

Задача

Груз Q=1000Н удерживается с помощью двух невесомых стержней, шарнирно скрепленных между собой в точке A и в шарнирах B и C с вертикальной стеной. Углы между стержнями и опорой: α=60°, β=30°.

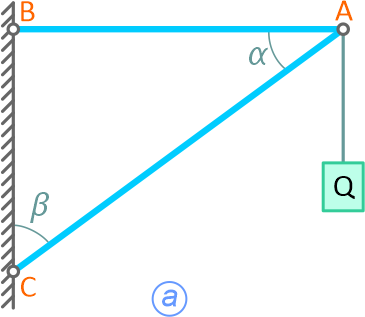
Требуется определить усилия в стержнях AB и BC.

Другие примеры решений задач

Решение

Видеоурок про реакции разных типов связей:

Другие видео

В данном случае следует рассмотреть равновесие точки A, т.к. все силы сходятся в этой точке.

Нить с грузом натянута силой Q. В равновесии точку A удерживают два невесомых стержня. Их реакции всегда направлены вдоль самих стержней.

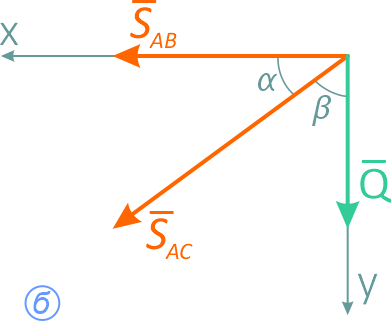
Реакции принято направлять от узла (точки A), т.е. предполагается, что стержни работают на растяжение (рисунок б). В случае отрицательного ответа при решении уравнений стержень работает на сжатие.

При равновесии системы сил выполняется равенство

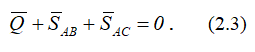
Это векторное равенство можно построить графически.

Откладываем в масштабе известную силу Q, к концу вектора прибавляем S_AB, т.к. его величина и направление неизвестны, проводим через конец вектора Q горизонтальную линию (параллельно S_AB, рисунок б).

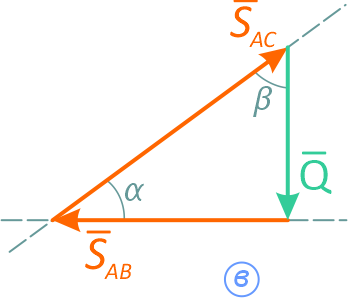
Замыкающий вектор S_AC должен пройти через начало вектора Q под углом β к вертикали.

Результатом построения является замкнутый треугольник (рисунок в).

Величины усилий в стержнях можно получить, умножая замеренные значения векторов сил на масштаб или воспользовавшись теоремой синусов:

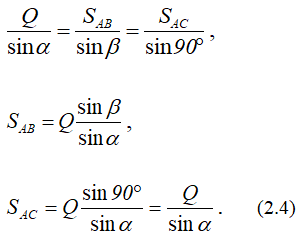
Направление силы S_AC в силовом треугольнике говорит о том, что этот стержень работает на сжатие.

Задача может быть решена и аналитически.

Для этого выбираем систему координат xAy (рисунок б) и проецируем на ее оси векторное равенство (2.3):

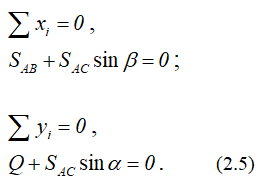
При этом

После решения уравнений равновесия находим значения усилий в стержнях AB и AC заданной системы

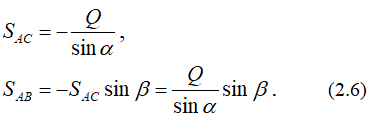
При решении, по знакам полученных усилий определяем, что стержень AC работает на сжатие, а стержень AB – на растяжение.

---

Дополнительно: