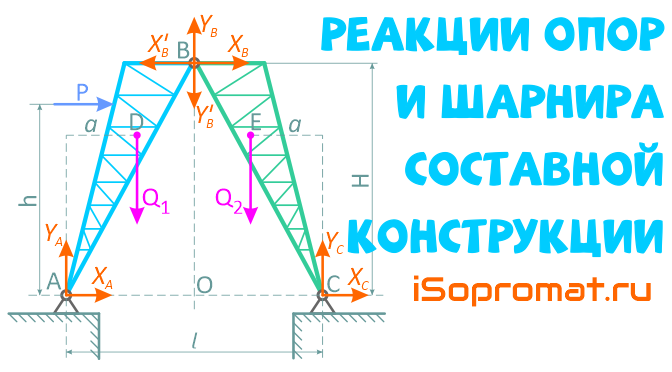
Пример решения задачи по определению реакций в опорах составной конструкции копра, состоящего из двух одинаковых ферм, соединенных между собой шарниром.
Задача
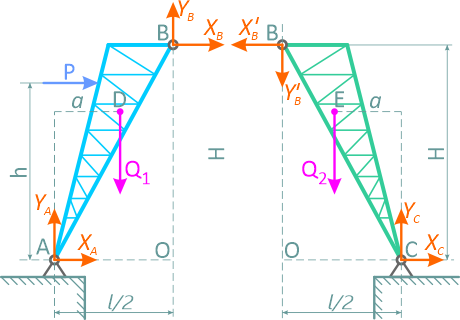
На рисунке 1 показана схема составной конструкции копра, состоящего из двух одинаковых ферм, соединенных между собой шарниром B. Веса этих ферм Q1 и Q2 равны и приложены в точках D и E.
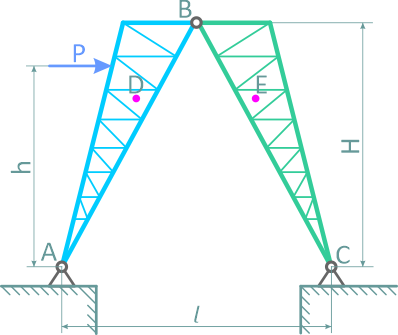
На левую ферму действует горизонтальная сила P давления ветра.
Требуется определить реакции в шарнирах A, B и C при указанных на рисунке размерах.
Пример решения
Направления реакций в шарнирах A, B и C составной конструкции неизвестны, а потому разложим каждую из них на горизонтальную и вертикальную составляющие, направив их, как указано на рисунке 2.
Пусть xB, yB − реакции левой фермы, приложенные к ферме C в точке B (шарнире, соединяющем две части конструкции), а xB′, yB′ − реакции правой фермы, приложенные в той же точке к ферме AB, причем xB′= -xB, yB′= -yB.
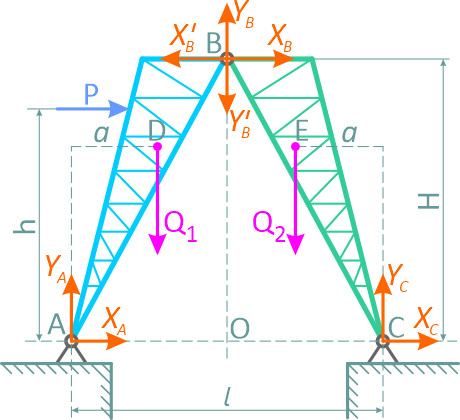
Так как в данном примере нужно найти шесть неизвестных реакций (xA, yA, xC, yC, xB, yB), то нужно составить шесть уравнений равновесия. Для этого сначала составим три уравнения равновесия для всей системы в целом (уравнения равновесия внешних сил xA, yA, xC, yC, P, Q1, Q2).
Приравнивая нулю сумму моментов сил относительно каждой из точек A и C составной конструкции и сумму проекций этих сил на ось x, получим:
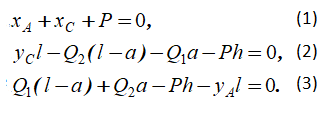
Правила знаков для сил и моментов.
Далее составим три уравнения равновесия отдельно для фермы BC (уравнения равновесия внешних сил xC, yC, xB, yB, Q2, приложенных к этой ферме). Приравнивая нулю сумму моментов этих сил относительно точки C и сумму их проекций на оси x и y, получим:
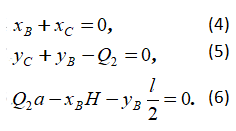
Решим полученную систему шести уравнений.
Из второго и третьего уравнений находим:
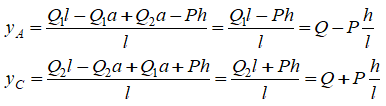
Из пятого уравнения:
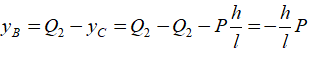
Из шестого уравнения:
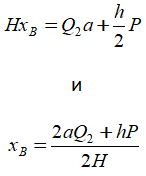
Из четвертого и первого уравнений получаем:
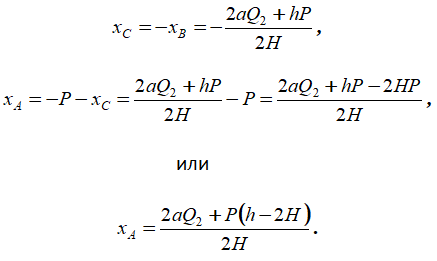
Далее, подставив значения нагрузок и размеров можно рассчитать величину реакций в опорах и шарнире составной конструкции.
Далее: