Решение задачи по определению реакций шарнирных опор прямой двухопорной балки длиной 16м с пролетом и консольной частью, нагруженной силой F, приложенной под углом α=35° к продольной оси x, а также изгибающим моментом M и равномерно-распределенной нагрузкой q по одному силовому участку.
Задача
Балка опирается на две шарнирные опоры: подвижную (правая) и неподвижную (левая).
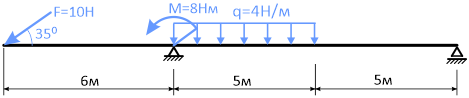
Требуется определить реакции в опорах.
Решение
Перед началом решения рекомендуется выполнить следующие действия:
- Изображаем балку в масштабе с опорами и действующими на нее нагрузками.
- Показываем оси системы координат х-y.
- Обозначаем характерные сечения балки буквами A, B, C и D.
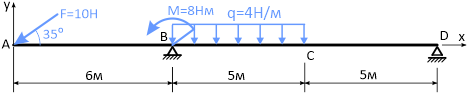
Для некоторого упрощения расчетов силу F можно заменить её горизонтальной и вертикальной проекциями (составляющими):
![]()
а распределенную нагрузку q — её равнодействующей:
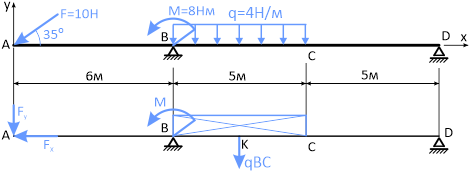
Равнодействующая qBC равномерно распределенной нагрузки, приложенная в точке пересечения диагоналей прямоугольника, переносится по линии своего действия в середину участка BC, в точку К.
Далее, освобождаем балку от шарнирных опор, заменив их опорными реакциями.
В левой (шарнирно-неподвижной) опоре будет две составляющие полной реакции, а в правой (шарнирно-подвижной) — только одна.
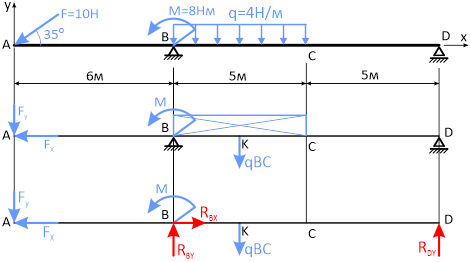
Составляем уравнения равновесия статики и определяем неизвестные опорные реакции.
Из уравнения равенства нулю суммы моментов всех действующих на балку сил, составленного относительно одной из точек опор (например, точки B),
![]()
определяем одну из неизвестных вертикальных реакций RDY:
![]()
Другую вертикальную реакцию определяем из суммы моментов сил относительно точки в опоре D:
![]()
откуда RBY
![]()
Горизонтальную реакцию RBX в опоре B рассчитаем из уравнения суммы проекций всех сил на горизонтальную ось x:
![]()
Проверяем правильность найденных результатов, проецируя все силы на вертикальную ось y. В сумме должен получиться ноль:
![]()
Условие равновесия выполняется, следовательно, реакции опор найдены верно.
Далее: