Распределенная нагрузка
Распределенной нагрузкой называют внешние или внутренние усилия, которые приложены не в одной точке твердого тела (т.е. не сосредоточены в одной точке), а равномерно, случайным образом или по заданному закону распределены по его определенной длине, площади (поверхности) или объему.
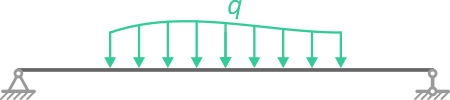
Интенсивность распределенной нагрузки — удельная величина усилия q, действующая на единицу длины, площади или объема элемента.
Рассмотрим виды распределенных нагрузок q: линейную, равномерную, треугольную (возрастающую или убывающую), трапециевидную, нелинейную, наклонную (направленную под углом) и замену их результирующей сосредоточенной силой — равнодействующей Q (Rq).
Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.
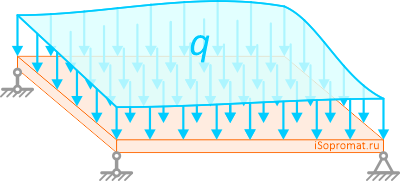
Это может быть собственный вес элемента конструкции, давление газа или воды, распределенный вес сыпучих материалов, ветровая нагрузка, снег и тому подобное.
Обозначение распределенной нагрузки — q или p (давление)
Размерность:
- линейной нагрузки — Н/м,
- нагрузки распределенной по площади — Н/м2,
- объемной (например при учете собственного веса элементов конструкции) — Н/м3.
или кратные им, например, кН/м.
Равнодействующая сила распределенной нагрузки
Равнодействующая распределенной нагрузки — воображаемая сосредоточенная сила Rq, которой при статических расчетах можно заменять действие распределенной нагрузки.
Эта замена необязательна и выполняется для некоторого упрощения вычислений, например, при составлении уравнений равновесия для определения реакций опор.
При решении некоторых задач технической и теоретической механики, распределенную нагрузку удобно заменять её равнодействующей, обозначаемой Q или Rq, которая для линейного случая распределения, определяется произведением средней интенсивности нагрузки q на её длину AB.
Для расчета величины равнодействующей силы распределенной нагрузки определяется площадь фигуры ограниченной профилем её распределения.
Равнодействующая распределенной нагрузки действует в точке элемента, расположенной под центром тяжести этой фигуры.
Рассмотрим виды распределенных нагрузок и способы их замены равнодействующей силой, сосредоточенной в одной точке.
Равномерно распределенная нагрузка
Равномерно распределенная нагрузка это нагрузка постоянной интенсивности (q=const) действующая продольно или поперечно оси элемента и распределенная по некоторой длине, площади или объему.
Такая нагрузка на схемах показывается в виде линейной группы небольших стрелок одинаковой длины, приложенных к рассматриваемому элементу или конструкции.
Равномерно распределенная по длине AB нагрузка интенсивностью q, измеряемая в Н/м
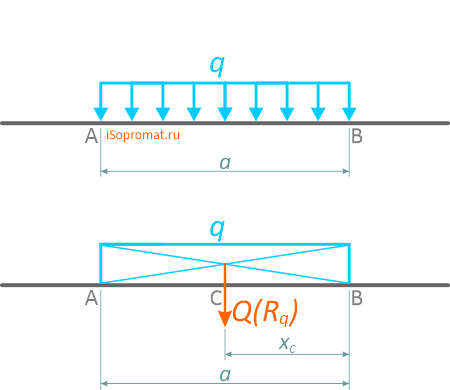
может быть заменена сосредоточенной силой Q (Rq)
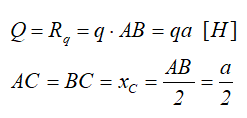
приложенной в центре (на пересечении диагоналей) прямоугольника, середине отрезка AB.
Материалы по теме:
- Как рассчитывается момент распределенной нагрузки относительно точки
- Пример решения задачи с распределенной нагрузкой
Линейно изменяющаяся (треугольная) нагрузка
Треугольная, поперечная линейно изменяющаяся убывающая (возрастающая) нагрузка
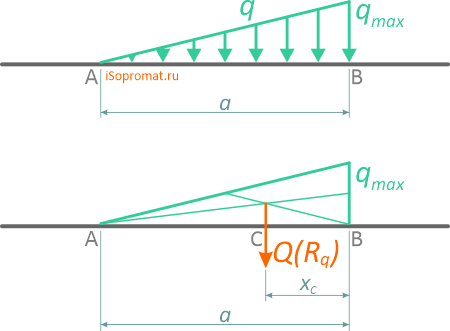
может быть заменена равнодействующей силой, приложенной в точке C
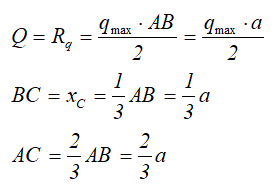
Отметим, что центр тяжести треугольника находится на пересечении его медиан, на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин.
Трапециевидная распределенная нагрузка
Трапециевидная, поперечная равномерно убывающая или возрастающая нагрузка характеризуется длиной и двумя значениями интенсивности распределения нагрузки: минимальной qmin и максимальной qmax
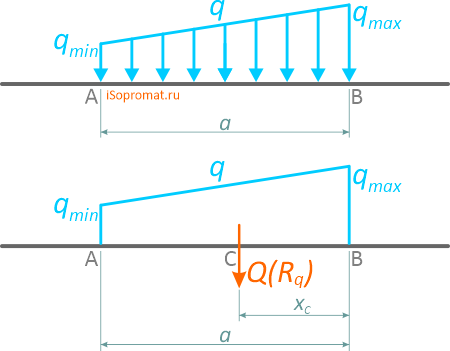
Профиль такой нагрузки представляет собой трапецию.
Величина и положение равнодействующей Q в данном случае определяется по выражениям
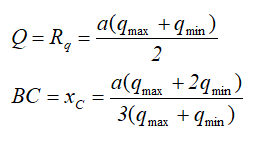
Нелинейная поперечная распределенная нагрузка
В произвольном общем случае, интенсивность распределения нагрузки по её длине может изменяться неравномерно и описываться одной или несколькими функциями.
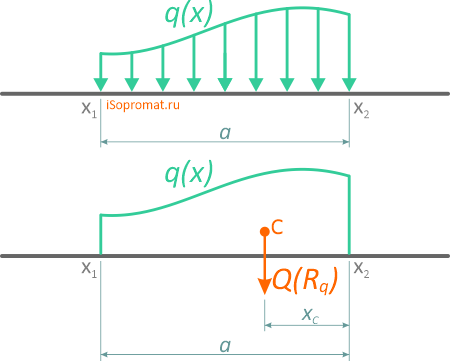
Зная функцию q(x), сосредоточенная эквивалентная (равнодействующая) сила рассчитывается по формуле
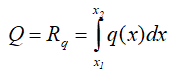
Эта сила также приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x).
Для расчета точки приложения равнодействующей нагрузки необходимо вычислить координату положения центра тяжести фигуры, образуемой нагрузкой.
Наклонная распределенная нагрузка
В случаях, когда распределенная нагрузка приложена под определенным углом, величина равнодействующей определяется аналогично ранее описанным способам.
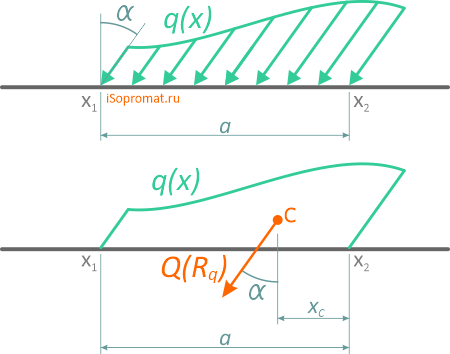
При этом угол наклона самой силы будет равен углу наклона нагрузки q.
Например, линия действия равнодействующей наклонной равномерно распределенной нагрузки будет пересекать ось балки ровно посередине между крайними точками её приложения.
Величина равнодействующей будет равна площади параллелограмма, образованного профилем нагрузки.
В отличие от рассмотренных ранее случаев, наклонная распределенная нагрузка может иметь две и более проекции на оси системы координат, одна их осей которой совмещена с осью элемента.
Распределенная нагрузка от давления
Примером распределенной нагрузки от давления p может служить расчет усилий, разрывающих стенки баллона со сжатым газом.
Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м];
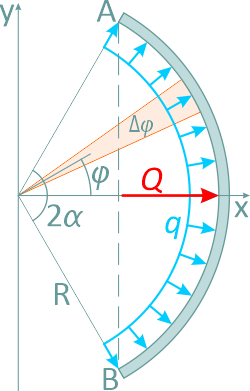
где:
R – радиус трубы,
2α – центральный угол,
ось Ox – ось симметрии.
Выделим элемент сектора с углом Δφ и определим силу ΔQ, действующую на плоский элемент дуги:
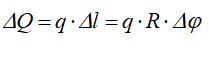
Проекция этой силы на ось Ox будет
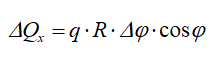
В силу симметрии элемента трубы (с дугой AB) относительно оси Ox проекция результирующей силы на ось Oy:
Qy = 0, т.е. Q = Qx,
Тогда
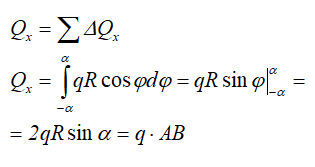
где АВ – хорда, стягивающая концы дуги.
Для цилиндрической емкости высотой h и внутренним давлением p на стенки действует равномерно распределенная нагрузка интенсивностью q = p [Н/м2].
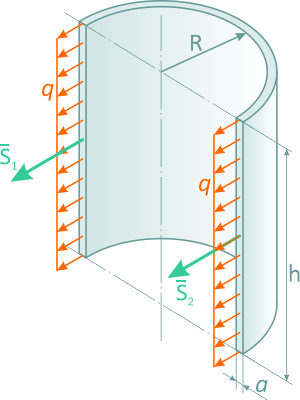
Если цилиндр рассечен по диаметру, то равнодействующая этих сил равна
F = q×d×h
где, d – внутренний диаметр, или
F = p×2R×h.
Тогда, разрывающие баллон по диаметру усилия:
S1 = S2 = S;
2S = F;
S = p×h×R.
Если принять что a – толщина стенки, то (пренебрегая усилиями в крышке и дне цилиндра) растягивающее напряжение в стенке равно
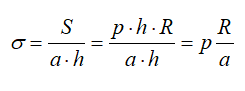
Далее:
