Теорема о скоростях точек в плоскопараллельном движении гласит: скорость любой точки плоской фигуры при плоскопараллельном движении равна геометрической сумме скорости выбранного полюса и скорости точки во вращательном движении фигуры вокруг полюса.
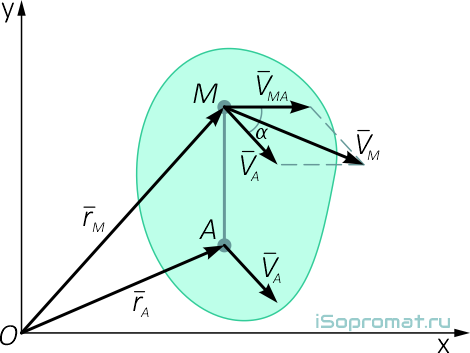
Рисунок 2.3
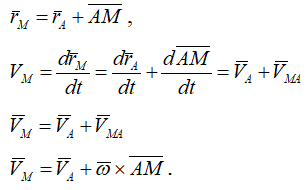
Производная от вектора AM, постоянного по величине и переменного по направлению, численно равна скорости точки М при вращении ее вокруг точки А.
![]()
Вектор
![]()
перпендикулярен отрезку АМ.
При плоскопараллельном движении, численную величину скорости точки М можно получить, если воспользоваться теоремой косинусов
![]()
или спроецировать векторное равенство (1) на выбранные оси координат
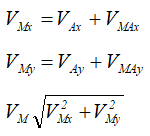
Далее: