Пример решения задачи по определению в заданный момент времени скорости, касательного и нормального ускорений и угла между вектором полного ускорения точки лежащей на ободе и радиусом диска, вращающегося по заданному закону.
Задача
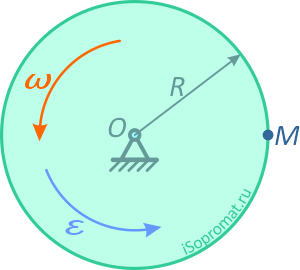
Диск радиуса R=0,5 м вращается по закону:
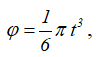
Требуется, в момент времени t=2 c определить скорость точки M, лежащей на ободе диска, её касательное и нормальное ускорение и угол между вектором ускорения и радиусом диска.
Решение
При заданном законе вращения угловая скорость и угловое ускорение определяются по формулам (2.3) и (2.4)
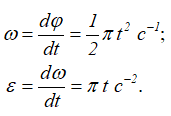
Для момента времени t=2 c:
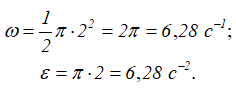
Скорость точки M:
![]()
Вектор скорости направлен по касательной к траектории движения точки, т.е. по касательной к окружности (рисунок 2.9).
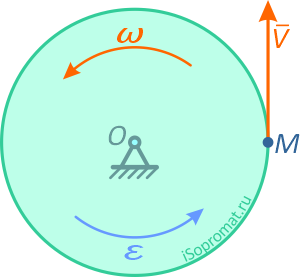
Ускорение точки M:
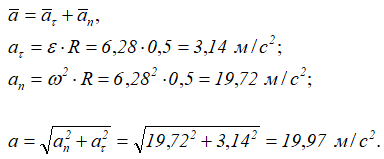
Касательное и нормальное ускорения направлены соответственно по касательной и по нормали (рисунок 2.10).
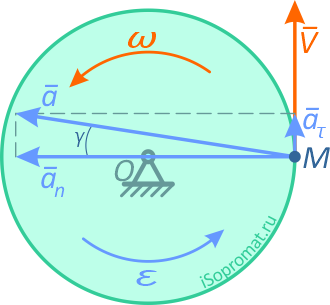
Угол между радиусом и вектором ускорения γ:
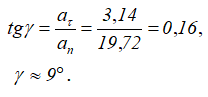
Далее: