Рассмотрим основные геометрические показатели и формулы при трении гибких тел.
Гибкие ленты, ремни, канаты и другие подобные материалы, оказывающие малое сопротивление при изгибе получили широкое применение в машинах в виде ременных и канатных приводов, а также в механизмах грузоподъемных машин, в ленточных тормозах.
При определении силы трения между барабаном и гибкой нитью (лентой) принимается следующее допущение – нить абсолютно гибкая и нерастяжимая. При таком допущении пренебрегают усилиями, затрачиваемыми на деформацию нити – ее изгиб и растяжение.
В этом случае, для того, чтобы нить перемещалась по барабану, к сбегающей ветви надо приложить усилие S2, преодолевающее усилие набегающей ветви S1 и силу трения между нитью и барабаном (рисунок 27):
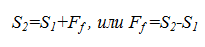
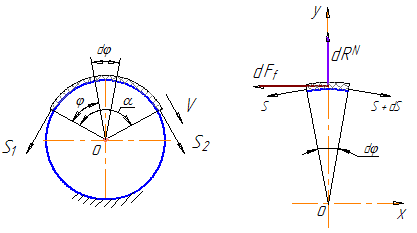
Центральный угол α, в пределах которого нить касается барабана, называется углом обхвата. Выделим элемент нити, стягиваемый центральным углом dφ, и рассмотрим его равновесие в проекциях на оси X и Y.
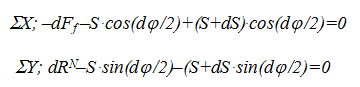
Заменив синус бесконечно малого угла самим углом (dφ/2), косинус бесконечно малого угла приравняв единице и, отбросив член второго порядка малости (произведение двух бесконечно малых величин dS∙cos(dφ/2)), после несложных преобразований получаем следующие зависимости:
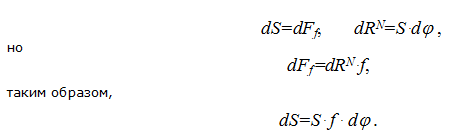
Разделив переменные, проинтегрируем полученное уравнение в пределах угла обхвата:
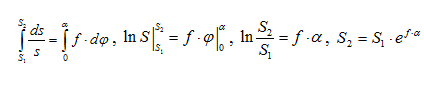
В результате сила трения между гибкой нитью (лентой) и барабаном определяется следующим образом:
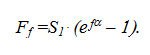
Эта формула получена Л. Эйлером и носит его имя.
В данном случае появляется дополнительный фактор – угол обхвата, с помощью которого можно существенно влиять на величину силы трения, что широко используется в технике.
Далее: