Рассмотрим порядок замены высших кинематических пар механизмов цепями с низшими парами.
Высшая кинематическая пара четвертого класса обеспечивает две степени свободы в относительном движении звеньев, поэтому данное относительное движение имеет сложный характер (оно включает в себя несколько взаимосвязанных простых движений).
В то же время низшая пара пятого класса обеспечивает простейшее относительное движение – вращательное или поступательное (эти два вида движения хорошо изучены и для их анализа разработаны относительно простые методы). Таким образом, с точки зрения методов исследования работы механизма, удобнее иметь дело с низшими кинематическими парами пятого класса.
Оказывается, что высшие пары четвертого класса можно заменить эквивалентными с точки зрения работы механизма цепями с низшими парами пятого класса. При этом необходимо выполнить следующие условия:
- число степеней свободы механизма при замене не должно изменяться;
- характер мгновенного относительного движения звеньев также должен оставаться прежним.
Для выполнения этих условий замена производится в следующем порядке (рисунок 6а):
- проводится общая нормаль к соприкасающимся профилям, составляющим высшую пару, в точке их контакта;
- определяется положение центров кривизны этих профилей в данной точке контакта и в каждом центре кривизны ставится шарнир;
- указанные шарниры соединяются жестким стержнем, в результате формируется фиктивное звено, которое в заданном механизме отсутствует;
- фиктивное звено указанными выше шарнирами присоединяется к тем звеньям механизма, которые входят в заменяемую высшую пару.
На рисунке 6 приведены примеры замены высшей кинематической пары для различных типов механизмов.
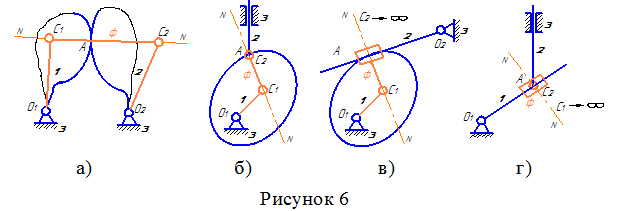
Примечания:
- имеются строгие доказательства того, что представленная последовательность действий обеспечивает выполнение условий, предъявляемых при замене высших пар. Однако в данном коротком курсе эти доказательства упущены;
- если профиль представляет собой одну единственную точку (профиль постоянно работает одной точкой), то его радиус кривизны равен нулю и центр кривизны находится в этой же точке (рисунок 6б);
- если профиль представляет собой прямую линию (работают разные точки этой прямой), то вместо шарнира ставится ползун, который движется вдоль этого прямолинейного профиля (действительно, центр кривизны прямолинейного профиля находится в бесконечности и шарнир, расположенный в бесконечности, обеспечивает вращательное движение с бесконечно большим радиусом вращения, т.е. поступательное движение. Таким образом, фиктивное звено с прямолинейным профилем соединяется поступательной кинематической парой) – рисунок 6в;
- на рисунке 6г приведен пример замены высшей пары, в котором, представлены обе особенности, отраженные в п.п. 2 и 3 данного примечания (в данном случае шарнир располагает непосредственно на ползуне);
- при замене высших кинематических пар лишние степени свободы автоматически исчезают. Поэтому, если при замене число степеней свободы уменьшилось, значит в механизме имеются лишние степени свободы. Таким образом, число степеней свободы заменяющего механизма совпадает с числом действующих (без лишних степеней свободы) степеней свободы заданного механизма (рисунок 7).
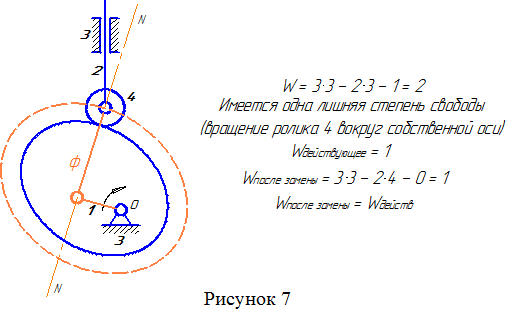
Каждая замена справедлива для данного мгновенного положения механизма. В другом положении замена будет аналогичной, но размеры звеньев заменяющей цепи изменятся, т.к. изменятся радиусы кривизны профилей в новой точке контакта. (Поэтому данный искусственный прием может использоваться только как метод исследования механизмов, но не как метод их проектирования).
Далее: