Рассмотрим порядок расчета уравновешивающего момента методом Н.Е. Жуковского.
Физический смысл уравнения Жуковского – сумма мгновенных мощностей, развиваемых силами и моментами, действующими на звенья механизма, равна нулю.
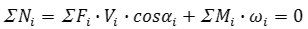
Для его составления прикладываем все силы в соответствующие точки плана скоростей, предварительно повернув их на 90 градусов (силы можно поворачивать в любую сторону, но все силы надо поворачивать в одну сторону – по часовой стрелке или против часовой стрелки).
Взяв, формально, сумму моментов этих повернутых сил относительно полюса плана скоростей, фактически получаем уравнение развиваемых ими мощностей. К полученному уравнению добавляем мощности, развиваемые моментами. При составлении уравнения Жуковского Н.Е. учитываем знак мощности, развиваемой данной силой или моментом:
- мощность, развиваемая силой, положительна, если эта сила является движущей, т.е. ее истинное направление составляет острый угол (меньше 90°) с направлением скорости точки приложения; мощность силы сопротивления (угол между истинным направлением силы и скорости точки ее приложения больше 90°) входит в уравнение Жуковского Н.Е. со знаком минус. Необходимо также отметить, что знак достаточно установить по одной силе, так как знаки остальных слагаемых определяются автоматически.
- мощность, развиваемая моментом, является положительной, если момент является движущим (его направление совпадает с угловой скоростью звена, к которому он приложен), и мощность отрицательна для момента сопротивления (направления момента и угловой скорости звена не совпадают).
Примечание: для составления уравнения Жуковского Н.Е. можно поворачивать на 90° план скоростей, прикладывая к нему силы в истинном направлении.
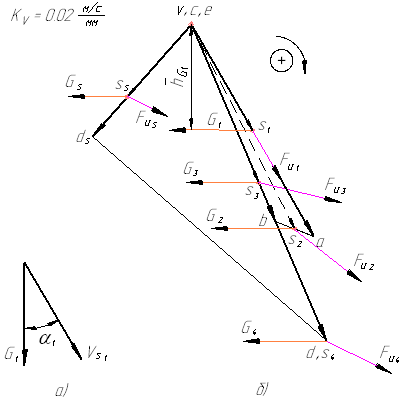
Рисунок 11 – Применение метода Н.Е. Жуковского для определения уравновешивающего момента
На рисунке 11 показана реализация данного метода на примере механизма, силовой расчет которого рассмотрен выше. В данном примере все силы, действующие на звенья механизма, повернуты по часовой стрелке и приложены в соответствующие точки плана скоростей, которые определяются методом подобия. Сначала определяем знак мощности какой-либо из сил, например, силы веса первого звена G1.
Истинное направление силы веса и скорости точки его приложения в данном случае составляют острый угол (рисунок 11а), поэтому данная сила развивает положительную мощность и в уравнение Н.Е. Жуковского эта мощность должна войти со знаком «плюс». Если рассматривать план скоростей как жесткий рычаг, то в повернутом состоянии сила G1 вращает его относительно полюса по часовой стрелке (рисунок 11б).
Таким образом, мощности сил, вращающих план скоростей по часовой стрелке, войдут в уравнение Н,Е. Жуковского со знаком «плюс», вращающие план против часовой стрелки – со знаком «минус».
Для определения знака мощности, развиваемой моментом, надо просто сравнить направление данного момента и угловой скорости звена, к которому он приложен (рисунки 5, 8, 9). При совпадении направлений момента и угловой скорости их произведение в уравнение входит со знаком «плюс», при разных направлениях – со знаком «минус».
Для приведенного примера (рисунок 11) уравнение Н.Е.Жуковского принимает следующий вид:
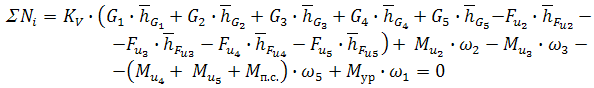
Далее: