Звездочки приводных цепей по конструкции во многом подобны зубчатым колесам. Делительная окружность звездочки проходит через центры шарниров цепи.

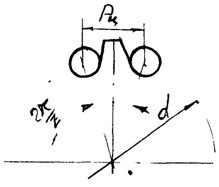
Диаметр этой окружности определяет равенство

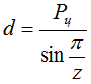
Формула справедлива и для звездочек зубчатых цепей.

Скорость цепи и частота вращения звездочки связаны по следующей формуле:

Передаточное отношение:

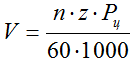
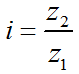
К.п.д. передачи — 0,96. Потери складываются из потерь на трение в шарнирах цепи, на зубьях звездочек и в опорах валов.

Межосевое расстояние по соображениям долговечности рекомендуется принимать

Длина цепи, выраженная в шагах или числом звеньев цепи:

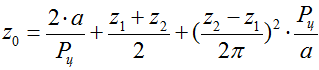
Значение z₀ округляют до целого четного числа, чтобы не применять специальных соединительных звеньев. Для принятого значения z₀ уточняют значение межосевого расстояния:

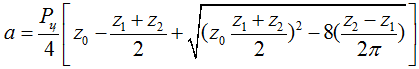
Передача работает лучше при небольшом провисании холостой ветви цепи. Поэтому расчетное межосевое расстояние рекомендуется уменьшить на (0,002…0,004)∙a.

Числа зубьев звездочек рекомендуется принимать в пределах

С уменьшением числа зубьев возрастают неравномерность скорости движения цепи и скорость удара цепи о звездочку. При этом увеличивается износ шарниров, т.к. угол поворота звена при набегании цепи на звездочку и сбегании с нее равен 360/z.

Выбирают z₁=29-2∙i

По мере износа цепи ее шарниры поднимаются по профилю зуба звездочки от ножки к вершине, что приводит, в конечном счете к нарушению зацепления. При этом, чем больше число зубьев звездочки тем меньше допустимое увеличение шага цепи.

Прочность цепных передач >
Содержание >