Основной закон зацепления профилей зубьев колес зубчатых передач гласит: для нормальной безотрывной работы передачи, составленной из двух профилей, входящих в высшую кинематическую пару, необходимо, чтобы нормаль к этим профилям в точке контакта в любой момент времени проходила через мгновенный центр их относительного вращения.

Зубья зубчатых колес составляют высшую пару IV класса, т.е. представляют собой некоторые поверхности, находящиеся в контакте.

Таким образом, профили зубьев – это кривые (а в некоторых случаях прямые) линии.

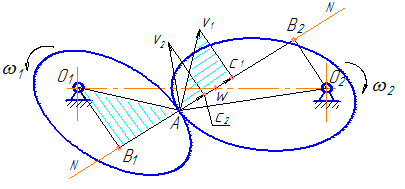
На рисунке 34 показаны два профиля, находящиеся в контакте в точке А. Скорость точки А, принадлежащей первому профилю (V₁), перпендикулярна радиусу О₁А, соответственно, скорость точки А, принадлежащей второму профилю (V₂), перпендикулярна радиусу О₂А.

Рассмотрим проекции этих скоростей на общую нормаль (N-N), проведенную к профилям в точке их контакта (С₁ – проекция скорости V₁ , С₂ – проекция скорости V₂). Могут получиться различные соотношения между значениями этих проекций:

Из рисунка 34 видно, что ΔAV₁C₁ подобен ΔO₁AB₁, и, соответственно, ΔAV₂C₂ подобен ΔO₂AB₂. Из подобия треугольников можно записать отношение сходственных сторон:

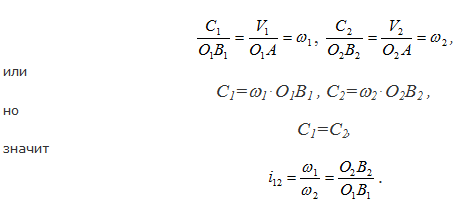
Здесь i₁₂ – передаточное отношение от первого профиля ко второму (это отношение угловой скорости на входе к угловой скорости на выходе).

Из подобия треугольников O₁B₁W и O₂B₂W (W – точка пересечения общей нормали N-N с линией центров O₁O₂) получаем:

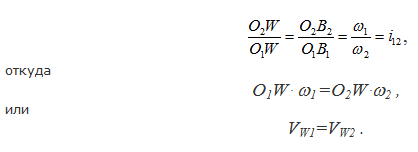
V_W1 – скорость точки W, связанной с первым профилем,
V_W2 – скорость точки W, связанной со вторым профилем.

Эти скорости совпадают не только по величине, но и по направлению (V_W1⊥O₁W, V_W2⊥O₂W, т.е. оба вектора перпендикулярны межосевому расстоянию O₁O₂).

Другие видео

Две точки совпадают по своему положению и имеют одинаковые скорости, то есть их относительная скорость равна нулю (V_W1W2=0). Таким образом, точка W является мгновенным центром относительного вращения рассматриваемых профилей.

Исходя из вышеизложенного, можно следующим образом сформулировать условие работоспособности передачи, составленной из двух профилей, входящих в высшую кинематическую пару:

— для нормальной безотрывной работы профилей необходимо, чтобы нормаль к этим профилям в точке контакта в любой момент времени проходила через мгновенный центр их относительного вращения.
Это условие носит название основного закона зацепления.

Профили, удовлетворяющие основному закону зацепления, называются сопряженными, а кривые которыми они описаны являются взаимоогибаемыми кривыми. При работе передачи взаимоогибаемые кривые перекатываются друг по другу со скольжением. Геометрическое место мгновенных центров скоростей, связанных с первым и вторым колесами, являются центроидами.

При работе передачи центроиды касаются в мгновенном центре относительного вращения и перекатываются друг по другу без скольжения. При постоянном передаточном отношении центроиды представляют собой окружности, которые в теории зацепления называются начальными окружностями.

Таким образом, передачи с постоянным передаточным отношением – это передачи с круглыми колесами, которые используются в большинстве случаев практики. В этом случае мгновенный центр при работе передачи не меняет своего положения и называется полюсом зацепления.

Элементы зубчатого зацепления

Стандартами на зубчатое зацепление вводятся определенные обозначения параметров:

Z – число зубьев колеса;
d – диаметр;
h – высота;
p – шаг (расстояние между одноименными профилями зубьев, измеренное по дуге какой-либо окружности);
S – толщина зуба (также измеряется по дуге окружности);
e – ширина впадины между зубьями;
a – межосевое расстояние.
Вводятся также буквенные индексы, показывающие, к какой окружности относится параметр:
w – начальная окружность;
b (или B) – основная окружность;
a – окружность вершин;
f – окружность впадин;
Y – окружность произвольного радиуса;

Без буквенного индекса – делительная окружность. Делительная окружность – это окружность, на которой шаг (и угол профиля) является стандартным:

Как видно из формул, вносить в стандарт непосредственно значения шага неудобно, т.к. при этом диаметр делительной окружности всегда будет величиной иррациональной (при изготовлении круглых деталей измеряют диаметры, поэтому надо, чтобы именно диаметры имели удобную величину). Поэтому в стандарт вводится величина, характеризующая отношение шага к числу π, которая называется модулем зацепления ( обозначается «m» и представлена в стандарте в миллиметрах).

Таким образом, основные параметры делительной окружности определяются следующими формулами:

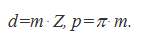
Модуль зацепления, с одной стороны обеспечивает условие взаимозаменяемости колес (работать в паре могут любые колеса одного модуля), с другой стороны определяет область применения зубчатых передач (передачи с m<1мм – мелкомодульные передачи – применяются в основном в небольших приборах; в общем машиностроении обычно применяют модули в пределах от 2мм до 5мм; модули более 10мм применяются в передачах тяжелого машиностроения).

Кроме буквенных индексов используются также индексы числовые. При расчете одной пары колес принято обозначать индексом «1» меньшее колесо пары (которое часто называют шестерней), индексом «2» – большее колесо.

Ниже приведены примеры обозначений параметров колес:

d_w1, d_w2 – диаметры начальных окружностей колес пары;
d_f1, d_f2 – диаметры окружностей впадин;
d₁, d₂ – диаметры делительных окружностей;
S₁ – толщина зуба на делительной окружности первого колеса;
S_a2 – толщина зуба на окружности вершин второго колеса;
S_Y1 – толщина зуба на произвольно выбранной окружности;
e_w1 – ширина впадины между зубьями на начальной окружности первого колеса;
h_aw1 – высота головки зуба первого колеса (часть зуба, расположенная вне начальной окружности);
h_wf2 – высота ножки зуба второго колеса (часть зуба, расположенная внутри начальной окружности);
a – делительное межосевое расстояние (сумма радиусов делительных окружностей);
a_w – межосевое расстояние (сумма радиусов начальных окружностей).

Следует обратить внимание на то, что шаги на начальных, делительных и основных окружностях для обоих колес пары одинаковы, поэтому в обозначениях этих параметров численный индекс отсутствует:

p_w1=p_w2=p_w – шаг на начальной окружности;
p₁=p₂=p – шаг на делительной окружности;
p_b1= p_b2=p_b – шаг на основной окружности (основной шаг).

Принятая система удобна, т.к. дает возможность по обозначению легко определить, что это за параметр и к чему он относится.

Кинематика зубчатых механизмов >
Курсовой проект по ТММ >