Определение величины момента M создаваемого равномерно распределенной нагрузкой q в произвольной точке балки.
Вопрос: Как определить момент в заданной точке балки, возникающий от распределенной нагрузки?

Ответ: При расчетах балок, в сопромате часто возникает задача определить изгибающий момент в сечениях балки вызванный действием равномерно распределенной нагрузки q.
В этом случае, как правило, удобнее пользоваться понятием равнодействующей силы Rq, которой можно заменить распределенную нагрузку.
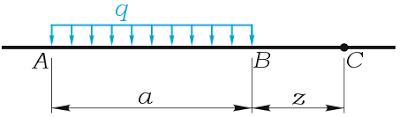
Рассмотрим пример нахождения момента в произвольной точке C от равномерно распределенной между точками A и B нагрузки интенсивностью q.
Для определения момента нагрузки необходимо знать ее длину a и расстояние z от любого ее края до рассматриваемой точки.
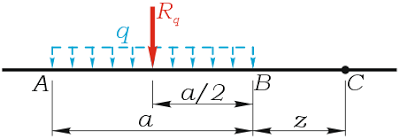
Заменим распределенную нагрузку ее равнодействующей Rq, которая для равномерного случая распределения будет располагаться ровно посередине нагрузки, при этом ее величина определяется как произведение интенсивности q нагрузки на ее длину a
Как известно момент силы определяется произведением силы на плечо
В данном случае силой в вышеуказанном выражении является равнодействующая Rq.
Плечом этой силы является расстояние от точки C до равнодействующей нагрузки
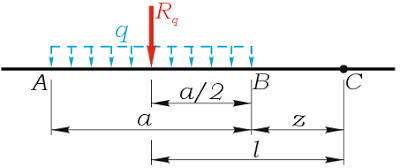
Таким образом, момент нагрузки равен произведению интенсивности q нагрузки на ее длину a и на расстояние от ее середины до рассматриваемой точки a/2+z
Для случая, когда точка лежит в пределах действия нагрузки, аналогично:
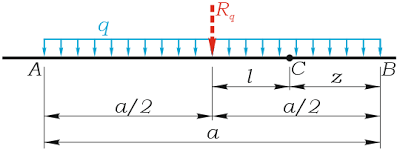
Примечания:
- В случае действия неравномерно распределенной нагрузки ее интенсивность задается функцией.
- Для нагрузки, распределенной по площади (объему) при вычислении равнодействующей вместо длины надо подставлять площадь (объем) ее действия.
- Момент части распределенной нагрузки определяется аналогично.
Далее: