Пример расчета допустимой растягивающей силы по условию прочности при продольном нагружении.

Задача

Рассчитать величину допустимой растягивающей внешней силы [F] приложенной к симметричной стальной пластине ослабленной тремя отверстиями.

Другие примеры решений >
Помощь с решением задач >

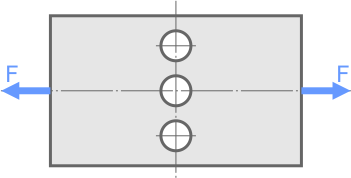
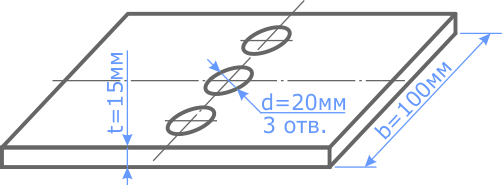
Размеры пластины: ширина b=100мм, толщина t=15мм. Диаметр отверстий d=20мм.

Принять допустимые напряжения для стали [σ]=120МПа.

Пример решения

Допустимой считается величина растягивающей силы, превышение которой приводит к нарушению прочности элемента.

Поэтому для решения задачи воспользуемся условием прочности при растяжении-сжатии:

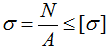
где σ — напряжения в элементе которые не должны превышать допустимых значений [σ],
N – внутренняя продольная сила,
А – площадь поперечного сечения элемента,

Запишем данное условие прочности относительно силового фактора

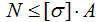
Заданная пластина имеет всего один силовой участок, поэтому внутренняя сила во всех ее сечениях будет одинакова и равна внешней силе F (N=F).

Следовательно, можно записать

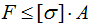
или

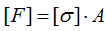
Прежде чем подставлять значения проанализируем заданную пластину.

По условию пластина ослаблена тремя отверстиями, поэтому очевидно, что наименее прочным будет поперечное сечение, проходящее через центры отверстий, где площадь минимальна.

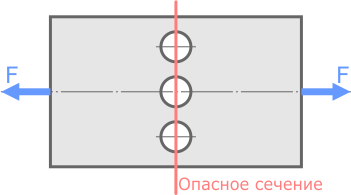
Рассчитаем минимальную площадь поперечного сечения пластины

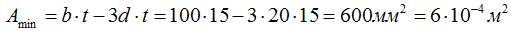
Теперь есть все данные для расчета допустимой силы:

Для того чтобы пластина оставалась прочной растягивающая сила должна быть не больше 72кН.

Превышение этого значения приведет к тому, что нормальные напряжения в опасном сечении превысят допустимые значения.

Другие примеры решения задач >