Циклическими координатами называются обобщенные координаты, которые не входят явно в выражение кинетического потенциала L.
Предположим, что среди обобщенных координат системы координаты q1, q2,… qk (k<s) являются циклическими.
Тогда по определению циклических координат производные от кинетического потенциала по этим координатам равны нулю. В этом случае k из s уравнений принимают вид
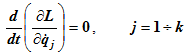
откуда
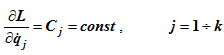
Последние равенства называются циклическим интегралами.
Циклические интегралы являются обыкновенными дифференциальными уравнениями первого порядка, решать которые намного проще, чем собственно уравнения Лагранжа второго рода.
Поэтому, выбирая обобщенные координаты, надо стремиться к тому, чтобы среди них было как можно больше циклических.
Далее: