Рассмотрим уравнения Лагранжа второго рода для механической системы имеющей одну степень свободы:
В случае если механическая система имеет одну степень свободы (s = 1), положение этой системы определяется одной обобщенной координатой q, которой соответствует обобщенная сила Q.
Уравнения Лагранжа второго рода для такой системы будут выглядеть так:
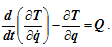
В случае, если система является консервативной (т.е. все активные силы, действующие на систему, являются потенциальными), уравнения Лагранжа второго рода для такой системы будут выглядеть так:
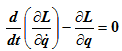
Для решения задач часто более удобна эквивалентная форма записи:
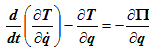
Чтобы составить уравнения Лагранжа второго рода для системы с одной степенью свободы, следует действовать в такой последовательности:
- сделать рисунок, обозначить на нем все активные силы, приложенные к системе;
- выбрать обобщенную координату q. При этом следует помнить, что от выбора обобщенной координаты зависит объем последующих вычислений. Если есть возможность, обобщенную координату следует выбрать так, чтобы она являлась циклической;
- определить, является ли рассматриваемая система консервативной;
- если система является консервативной, следует вычислить ее кинетическую T и потенциальную энергию Π, выразив их через обобщенную координату q и обобщенную скорость q’. Если система не является консервативной, следует вычислить только ее кинетическую энергию;
- вычислить производные, входящие в уравнения Лагранжа второго рода.
Если система не консервативная, это будут производные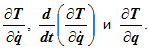
Если система консервативная, к ним добавится производная ∂Π/∂q;
- определить обобщенную силу Q. Если система консервативная, этот пункт следует пропустить;
- все найденные производные и обобщенную силу подставить в уравнение Лагранжа второго рода для системы с одной степенью свободы, в формулировке для консервативной или неконсервативной системы.
Далее: