Уравнения Лагранжа второго рода, которые представляют собой дифференциальные уравнения второго порядка относительно обобщенных координат.

Рассмотрим механическую систему, имеющую s степеней свободы, на которую наложены стационарные, идеальные, голономные связи.

В этом случае положение системы определяется s обобщенными координатами q₁, q₂,…q_s.
Кинетическая энергия такой системы является функцией обобщенных координат q₁, q₂,…q_s, обобщенных скоростей

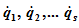
и времени

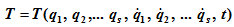
Для такой системы можно записать s уравнений, которые называются уравнениями Лагранжа второго рода или дифференциальными уравнениями движения в обобщенных координатах:

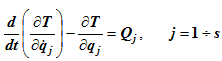
Уравнения Лагранжа второго рода могут быть обобщены на случай связей, осуществляемых с трением, хотя они и не являются идеальными. Для этого следует силу трения перенести из группы сил реакции в группу активных сил, тогда связь с трением можно формально считать идеальной.

Уравнения Лагранжа второго рода представляют собой дифференциальные уравнения второго порядка относительно обобщенных координат q₁, q₂,…q_s.

Дважды интегрируя эти уравнения и определяя по начальным условиям постоянные интегрирования, получим систему уравнений движения в обобщенных координатах:

Дополнительно:

• Примеры решения задач >
• Уравнения Лагранжа второго рода для систем с одной степенью и двумя степенями свободы
• Кинетический потенциал