Составление систем дифференциальных уравнений относительного движения точки массой m под действием сил.

Уравнение второго основного закона динамики для абсолютного движения точки массой m имеет вид

где a – абсолютное ускорение точки;
F_i – силы, действующие на точку, включая реакции связей.

Абсолютное ускорение точки в сложном движении определяется как геометрическая сумма трех ускорений: переносного a_пер , относительного a_отн и кориолисова a_кор, т.е.

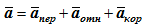
Подставляя это выражение в (7.1), получим

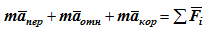
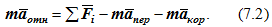
Введем в рассмотрение два вектора

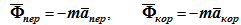
и назовем их переносной и кориолисовой силами инерции.

Подставим эти векторы в уравнение (7.2):

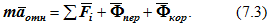
Уравнение (7.3) представляет собой основное уравнение динамики относительного движения материальной точки.

В случае равномерного и поступательного переносного движения Ф_пер= 0, Ф_кор= 0 и уравнение (7.3) ничем не отличается от уравнения (7.1). Во всех инерциальных системах отсчета уравнение движения точки записывается одинаково. В этом заключается принцип относительности классической механики.

Проецируя уравнение (7.3) на оси подвижной декартовой системы координат, получим дифференциальные уравнения относительного движения точки

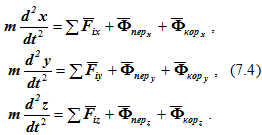
Дифференциальные уравнения относительного движения отличаются от дифференциальных уравнений абсолютного движения наличием в правой части уравнений проекций на соответствующие оси переносной и кориолисовой сил инерции.

Рассмотрим частные случаи относительного движения материальной точки:

1. если подвижная система отсчета движется поступательно, то Ф_кор= 0, так как ω_пер= 0, и уравнение относительного движения примет вид
   ma_отн=ΣF_i +Ф_пер     (7.5)
2. если точка по отношению к подвижным осям находится в покое, то для нее a_отн=0, V_отн=0 и, следовательно, Ф_кор=0. Тогда уравнение (7.3) примет вид
   ΣF_i+Ф_пер=0     (7.6)

Уравнение (7.6) представляет собой уравнение относительного покоя точки.

Примеры решения задач >
Кинетическая энергия >