Рассмотрим теорему об изменении количества движения механической системы состоящей из материальных точек:
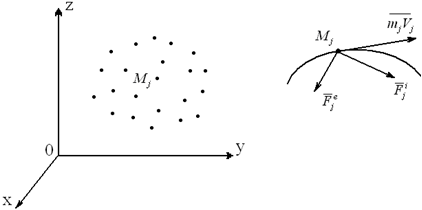
Пусть имеем механическую систему, состоящую из n материальных точек. Выделим из этой системы некоторую точку Mj с массой mj. На эту точку, как известно, действуют внешние и внутренние силы.
Приложим к точке Mj равнодействующую всех внутренних сил Fji и равнодействующую всех внешних сил Fje (рисунок 2.2). Для выделенной материальной точки Mj (как для свободной точки) запишем теорему об изменении количества движения в дифференциальной форме (2.3):
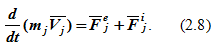
Запишем аналогичные уравнения для всех точек механической системы (j=1,2,3,…,n).
Сложим почленно все n уравнений:
Здесь ∑mj×Vj =Q – количество движения механической системы;
∑Fje = Re – главный вектор всех внешних сил, действующих на механическую систему;
∑Fji= Ri =0 – главный вектор внутренних сил системы (по свойству внутренних сил он равен нулю).
Окончательно для механической системы получаем
Выражение (2.11) представляет собой теорему об изменении количества движения механической системы в дифференциальной форме (в векторном выражении) которая гласит: производная по времени от вектора количества движения механической системы равна главному вектору всех внешних сил, действующих на систему.
Проецируя векторное равенство (2.11) на декартовы оси координат, получаем выражения для теоремы об изменении количества движения механической системы в координатном (скалярном) выражении:
dQx/dt = Rxe;dQy/dt = Rye;dQz/dt = Rze, (2.12)
т.е. производная по времени от проекции количества движения механической системы на какую-либо ось равна проекции на эту ось главного вектора всех действующих на эту механическую систему внешних сил.
Умножая обе части равенства (2.12) на dt, получим теорему в другой дифференциальной форме:
т.е. дифференциал количества движения механической системы равен элементарному импульсу главного вектора (сумме элементарных импульсов) всех внешних сил, действующих на систему.
Интегрируя равенство (2.13) в пределах изменения времени от 0 до t, получаем теорему об изменении количества движения механической системы в конечной (интегральной) форме (в векторном выражении):
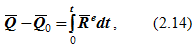
т.е. изменение количества движения механической системы за конечный промежуток времени равно полному импульсу главного вектора (сумме полных импульсов) всех внешних сил, действующих на систему за тот же промежуток времени.
Проецируя векторное равенство (2.14) на декартовы оси координат, получим выражения для теоремы в проекциях (в скалярном выражении):
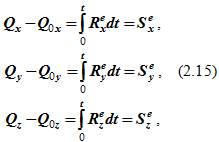
т.е. изменение проекции количества движения механической системы на какую-либо ось за конечный промежуток времени равно проекции на эту же ось полного импульса главного вектора (сумме полных импульсов) всех действующих на механическую систему внешних сил за тот же промежуток времени.
Из рассмотренной теоремы (2.11) – (2.15) вытекают следствия:
- Если Re = ∑Fje = 0, то Q = const – имеем закон сохранения вектора количества движения механической системы: если главный вектор Re всех внешних сил, действующих на механическую систему, равен нулю, то вектор количества движения этой системы остается постоянным по величине и направлению и равным своему начальному значению Q0, т.е. Q = Q0.
- Если Rxe = ∑Xje=0 (Re ≠ 0), то Qx = const – имеем закон сохранения проекции на ось количества движения механической системы: если проекция главного вектора всех действующих на механическую систему сил на какую-либо ось равна нулю, то проекция на эту же ось вектора количества движения этой системы будет величиной постоянной и равной проекции на эту ось начального вектора количества движения, т.е. Qx = Q0x.
Дифференциальная форма теоремы об изменении количества движения материальной системы имеет важные и интересные приложения в механике сплошной среды. Из (2.11) можно получить теорему Эйлера:
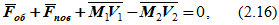
где M – секундная масса – масса среды, протекающей через какое-либо сечение трубы в единицу времени. Размерность секундной массы в системе СИ равна кг∙с-1;
Fоб – главный вектор внешних объемных сил;
Fпов – главный вектор внешних поверхностных сил;
V1, V2 – скорости частиц среды, протекающих через соответствующие поперечные сечения.
Примеры решения задач >
Теорема об изменении момента количества движения (кинетического момента) материальной точки >
