Мгновенный центр скоростей (МЦС) — при плоскопараллельном движении связанная с плоской фигурой или твердым телом точка, скорость которой в данный момент равна нулю.

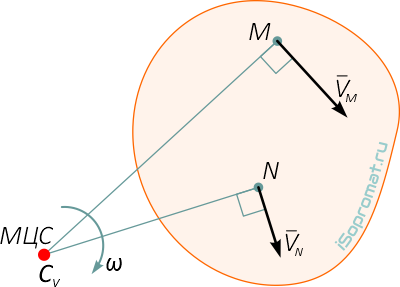
Другими словами МЦС это положение точки, относительно которой происходит поворот тела в заданном положении и в данный момент времени.

В этот момент скорости всех точек тела пропорциональны расстоянию до мгновенного центра скоростей.

Точка положения МЦС обозначается латинскими буквами C или P с нижним индексом V, например, C_V или P_V.

Такая точка существует в каждый момент времени движения тела, меняя свое положение.

В некоторых случаях (при поступательном движении тела) точка МЦС удаляется на бесконечно большое расстояние (будет рассмотрено ниже).

Теорема Эйлера-Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра.

В соответствии с этим легко доказывается, что при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю. Эту точку называют мгновенным центром скоростей.

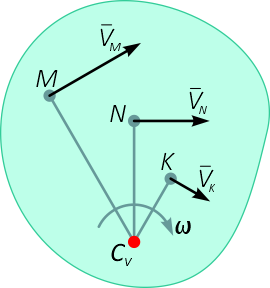
При определении положения МЦС скорость любой точки может быть записана:

где точка C_V выбрана за полюс.

Поскольку это МЦС и V_CV=0, то скорость любой точки определяется как скорость при вращении вокруг мгновенного центра скоростей:

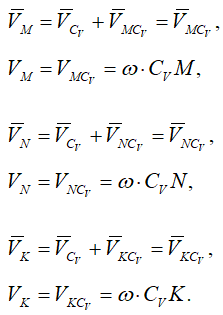
Из рис. 17 видно, что мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных к скоростям точек, при этом всегда справедливо соотношение

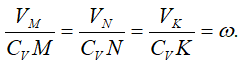
Далее показаны положения мгновенного центра скоростей и приведены формулы для расчета скоростей точек.

Для звена AB кривошипно-шатунного механизма:

Кривошип OA вращается относительно точки O, поэтому скорость точки A всегда направлена по касательной к окружности радиусом OA.

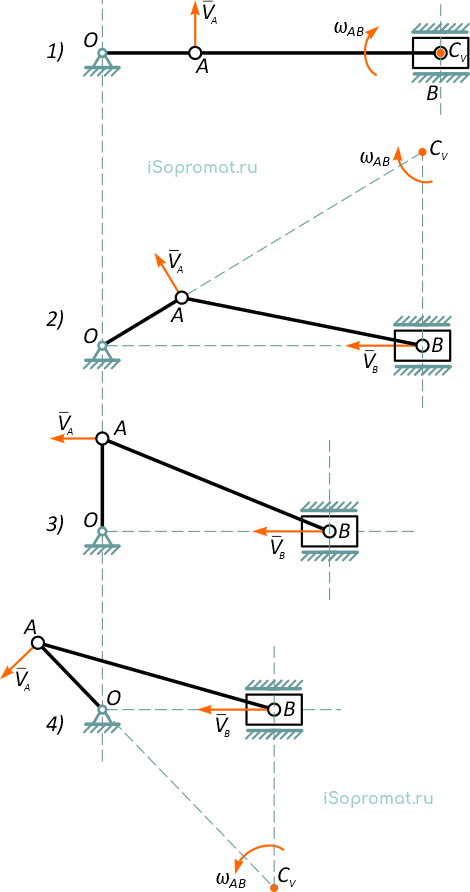
Положение 1.

Частный случай 1, C_V совпадает с точкой B скорость которой в данном положении V_B=0. Шатун AB вращается вокруг точки B.

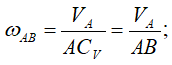
Положение 2.

Мгновенный центр скоростей находится в точке пересечения линий, перпендикулярных направлению скоростей точек A и B.

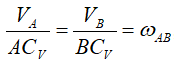
Положение 3.

Частный случай 2, МЦС отдалён в «бесконечность», т.к. векторы скоростей параллельны.

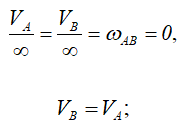
Положение 4.

Аналогично положению 2.

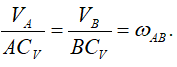
Пример определения мгновенного центра скоростей

МЦС при вращении тел и фигур:

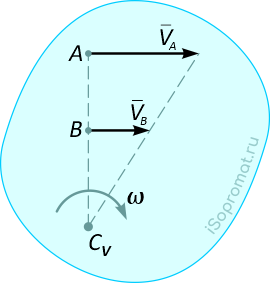
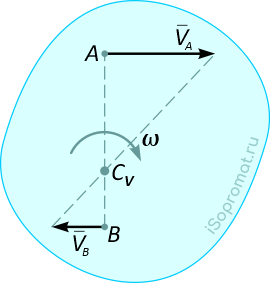
Для этих случаев

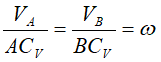
При прямолинейном и поступательном движении:

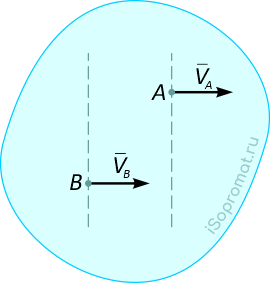
Здесь векторы скоростей точек равны и параллельны

В этом случае МЦС находится в “бесконечности”, т.е.

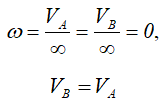
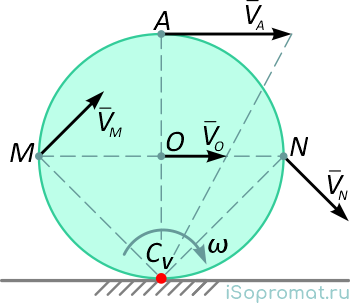
При качении тел мгновенный центр скоростей находится в точке контакта колеса с поверхностью:

Колесо или цилиндр радиусом R катится по ровной поверхности.

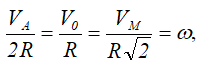
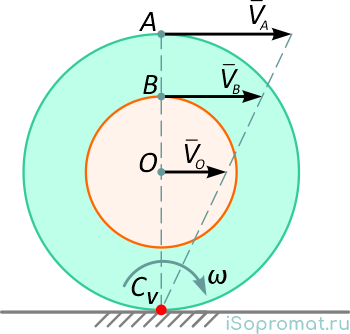
Сдвоенное колесо (или кольцо) с радиусами R и r.

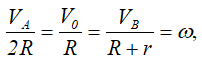
Колесо с гребнем (ребордой).

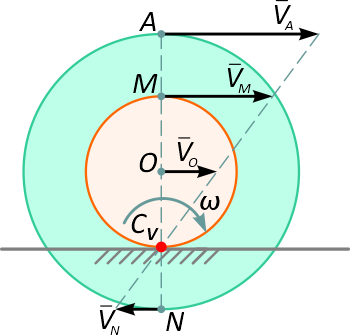
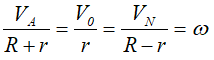
Формулы справедливы при отсутствии проскальзывания в точке C_V.

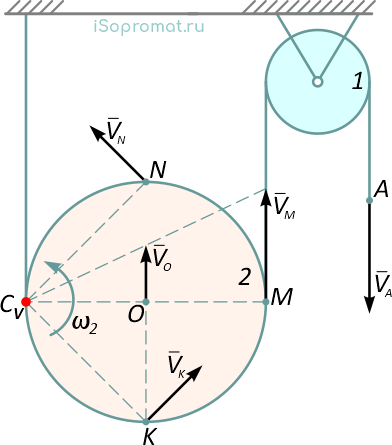
МЦС системы подвижных блоков:

Нерастяжимая нить удерживает подвижный блок 2 и перемещается через неподвижный блок 1.

Для простого блока

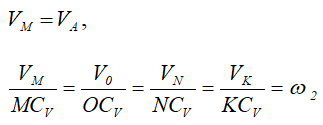
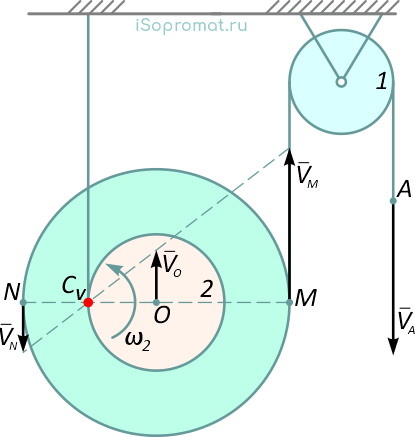
Для двойного блока

---

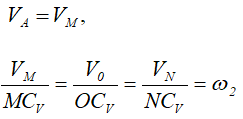
Далее: