Первая, основная задача динамики точки заключается в том, чтобы по заданному закону движения материальной точки определить результирующую или одну из составляющих сил, действующих на эту точку.
В основе классической динамики лежат законы, впервые сформулированные и систематически изложенные Исааком Ньютоном в его «Математических началах натуральной философии».
В зависимости от того, что нам известно и что необходимо найти, в динамике рассматривают две основные задачи.
При наличии нескольких сил, действующих на точку, второй закон Ньютона дает основное уравнение динамики точки
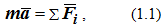
где m – масса точки;
a – ускорение точки;
Fi – силы, действующие на точку.
В зависимости от способа задания движения точки, это уравнение можно записать по-разному.
Для векторного способа задания движения
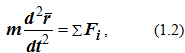
где r = r (t) – радиус-вектор, определяющий положение точки по отношению к выбранной системе отсчета.
Для координатного способа задания движения точки
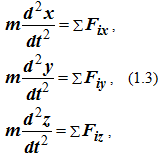
где x = x(t), y = y(t), z = z(t) – координаты точки, заданные как функции времени.
Для естественного способа задания движения точки
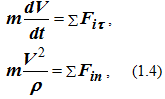
где dV/ dt – проекция ускорения точки на касательную в данной точке (касательное ускорение),
V2/ ρ – проекция ускорения на нормаль (нормальное ускорение),
ρ – радиус кривизны траектории.
В правой части уравнений – проекции сил на касательную ΣFiτ , нормаль ΣFin и бинормаль ΣFib.
По заданному закону движения точки определяются правые части этих уравнений, и далее может быть определена результирующая сила
- при координатном способе задания движения:
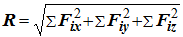
- при естественном способе или одна из составляющих сил:
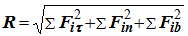
Направление силы определяется с помощью направляющих косинусов:
cos (α) = Rx / R
cos (β) = Ry / R
cos (γ) = Rz / R
где α, β, γ – углы между направлением силы и осями x, y, z соответственно.
Аналогично определяются углы, которые составляют силы с естественными осями координат.
Далее: