Любую систему сил инерции точек твердого тела можно привести к выбранному центру масс или к любому другому центру системы.

В разделе «Статика» на основании принципа Пуансо показывается, как любая система сил может быть приведена к выбранному центру (полюсу) и заменена на главный вектор, равный геометрической сумме всех сил, и главный момент, равный моменту всех сил относительно центра приведения.

При приведении системы сил к центру масс получается главный вектор сил инерции:

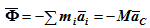
и главный момент сил инерции

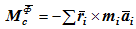
Рассмотрим частные случаи движения твердого тела.

При поступательном движении ускорения всех точек равны и одинаково направлены, т.е. имеется система параллельных сил инерции, результирующая которых приложена в центре масс и равна

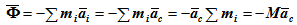
Момент инерциальных сил относительно центра масс равен нулю.

При вращении твердого тела вокруг неподвижной оси, проходящей через центр масс, главный вектор сил инерции Ф = 0 (a_c = 0), а главный момент получается равным

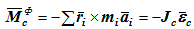
В случае плоскопараллельного движения твердого тела система сил инерции приводится к главному вектору сил инерции, приложенному в центре масс и равному

Ф = -M × a_c

и к главному моменту сил инерции, равному

M_c^ф = -J_c × ε_c.

Примеры решения задач >
Возможные перемещения >