Возможными (виртуальными) перемещениями несвободной механической системы называются воображаемые, бесконечно малые перемещения точек системы, допускаемые наложенными на систему связями.
Возможные перемещения – это величины первого порядка малости, величинами высших порядков малости пренебрегаем, поэтому криволинейные перемещения точек заменяются прямолинейными отрезками, откладываемыми в направлении касательной к траектории каждой точки.
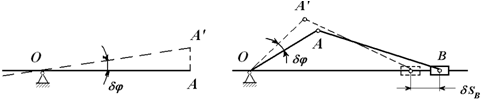
Возможные перемещения обозначаются символом «δ». Например, δφ, δS (рисунок 2.1), для точки A:
δSA = AA’ = OAδφ.
Все силы, действующие на точки несвободной механической системы, могут быть разделены на задаваемые силы и реакции связей. Задаваемые силы выражают действие на механическую систему тел, не входящих в данную систему. Реакции связей выражают действие связей, ограничивающих движение системы (рисунок 2.2).
Если сумма работ реакций связей на любом возможном перемещении системы равна нулю, то такие связи называют идеальными, т.е.
∑Ri ⋅ δSi ⋅ cosαi= 0.
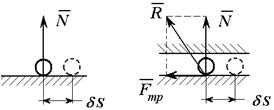
На рисунке 2.2 при перемещении тела на величину δS (возможное перемещение) работа реакции для гладкой поверхности связи:
δA=N⋅ δS⋅ cos90o =0
т.е. эта связь идеальна. В случае шероховатой поверхности появляется сила трения и полная реакция такой поверхности будет
R = N + FТР
Работа этих двух сил уже не равна нулю.
δA = FТР⋅ δS⋅ cos180o.
Чтобы выведенные в механике принципы можно было применять в реальных задачах, нужно неидеальные связи искусственно сделать идеальными, отнеся силы трения к разряду задаваемых сил.
Далее: