Связями в механике называются любого вида ограничения, накладываемые на положения, скорости точек механической системы, независящие от действующих сил.
Связи неизменяемые со временем называются стационарными, изменяемые – нестационарными.
Связи бывают удерживающие, когда ограничения сохраняются при любом положении системы и неудерживающие, которые этим свойством не обладают.
Связи, налагающие ограничения на координаты точек системы называются геометрическими, а накладывающие ограничения на скорости точек системы кинематическими или дифференциальными.
Если дифференциальную связь можно представить как геометрическую (проинтегрировать), то такая связь называется интегрируемой, в противном случае не интегрируемой.
Геометрические интегрируемые дифференциальные связи называются голономными, а неинтегрируемые дифференциальные связи неголономными. Соответственно и системы разделяют на голономные (с голономными связями) и неголономные (с неголономными связями).
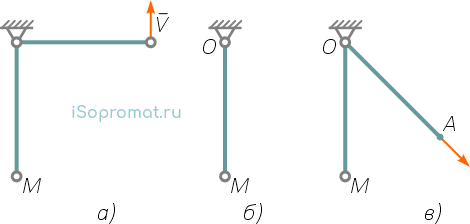
Рисунок 11
Пример: на рисунке 11а, шарик М в плоскости закреплен через стержень с шарниром О – стационарная удерживающая голономная связь V = ω × l, интегрируем S = φ × l.
Рисунок 11б, – ОМ – нить, – в этом случае это неудерживающая, стационарная связь.
Рисунок 11в, – нить продернута в кольцо О, конец А нити движется со скоростью u — неудерживающая нестационарная связь, ее уравнение:
![]()
Эффект механических связей можно учитывать и рассматривая перемещения, которые допускаются наложенными связями. Возможными перемещениями механической системы называется любая совокупность элементарных (бесконечно малых) перемещений точек системы из занимаемого в данный момент времени положения, которое допускается наложенными на систему связями.
Связи называются идеальными, если сумма элементарных работ их реакций на любом возможном перемещении равна нулю.
Например: тело на гладкой поверхности (рисунок 12), реакция опоры направлена по нормали к поверхности, δS — возможное перемещение.
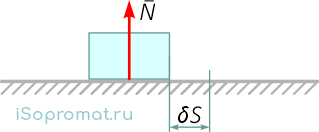
Рисунок 12
Элементарная работа реакции связи:
![]()
т.е. связь идеальна.
Далее: