Рассмотрим определение величины и направления скоростей и ускорений точек при сложном движении.

Теоремы о скоростях и ускорениях точек в сложном движении подробно изложены в учебниках по теоретической механике.

Абсолютная скорость точки при сложном движении определяется как геометрическая сумма переносной и относительной скоростей:

Каждое слагаемое в этой формуле определяется независимо друг от друга, исходя из соответствующего закона движения. В примере на рисунке 3 относительная скорость V_r определяется с учетом закона движения точки по оси Oy.

Переносная скорость определится как скорость точки M при вращении вместе с квадратом вокруг оси его вращения. Величина абсолютной скорости может быть определена с помощью теоремы косинусов:

Для определения вектора абсолютной скорости можно равенство (1) спроецировать на выбранные оси координат, найти проекции абсолютной скорости, её величину и направляющие косинусы, то есть определить углы, которые вектор скорости составляет с выбранными осями.

Ускорение точки при сложном движении определяется как сумма трех ускорений: переносного, относительного и кориолисова (поворотного):

Первые два слагаемых этой формулы определяются из соответствующих законов переносного и относительного движений. В случае неравномерных криволинейных движений эта формула имеет вид

Кориолисово ускорение определяется по формуле:

Величина этого ускорения

где α — угол между векторами переносной угловой и линейной относительной скоростями.

Направление кориолисова ускорения определяется двумя правилами:

Правило векторного произведения

Согласно правилу векторного произведения, вектор кориолисова ускорения перпендикулярен векторам ω_e и V_r (или плоскости, проходящей через эти вектора, проведенные из одной точки). Направлен вектор a_K так, что если смотреть ему навстречу, то кратчайший поворот вектора ω_e до совмещения с вектором V_r происходит против хода часовой стрелки (рисунок 1).

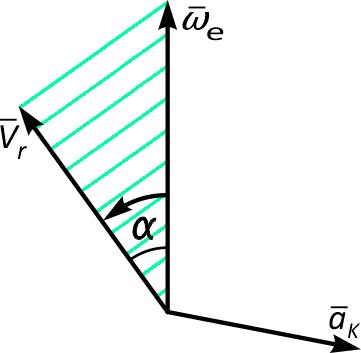
Правило Жуковского

Для определения направления кориолисова ускорения при сложном движении нужно спроецировать вектор относительной скорости в плоскость, перпендикулярную вектору переносной угловой скорости и полученную проекцию повернуть в сторону переносного вращения (рисунок 2).

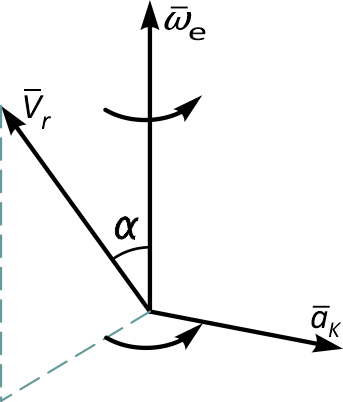
Из формулы (5) видно, что кориолисово ускорение равно нулю, если

• равна нулю относительная скорость;
• переносное движение — поступательное (ω_e=0);
• угол между ω_e и V_r равен 0° или 180° (вектор V_r параллелен оси переносного вращения).

Абсолютное ускорение точки при сложном движении определяется по аналогии с определением её скорости. Формула (3) проецируется на выбранные оси координат и находятся проекции абсолютного ускорения на эти оси: a_x, a_y, a_z.

Величина ускорения определяется по формуле:

Направление вектора абсолютного ускорения определяется с помощью направляющих косинусов, то есть определяются углы, которые вектор ускорения составляет с осями координат:

---

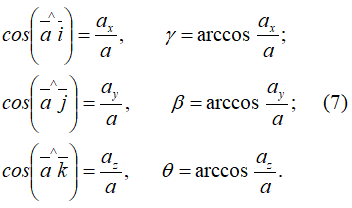
Далее: