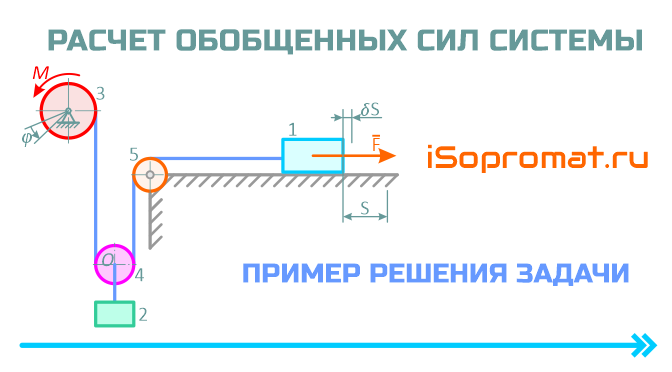
Пример решения задачи по определению величины обобщенных сил механической системы приводящейся в движение силой F и моментом M, с невесомыми блоками.
Задача
Механическая система приводится в движение силой F и моментом M.
Дано: m1, f, m2, r3, F. Блоки 3, 4, 5 – невесомые.
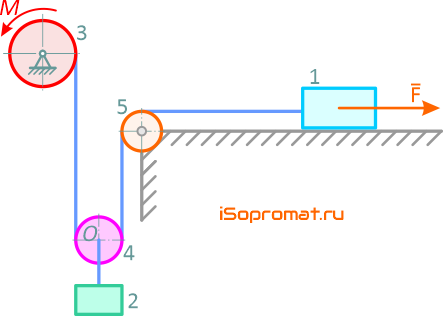
Требуется определить обобщенные силы механической системы.
Пример решения
Система имеет две степени свободы. Введем обобщенные координаты: s — перемещение груза 1, φ — угол поворота блока 3.
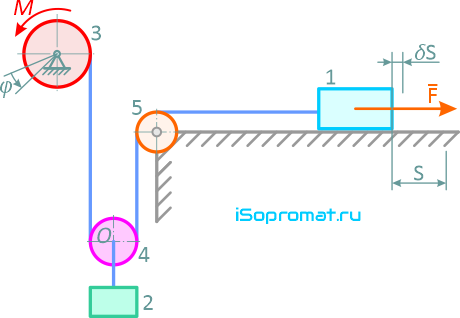
Определим обобщенную силу, соответствующую обобщенной координате s, для этого зададим ей малое приращение δs (угол φ — не меняется!). Силы, приложенные к системе, совершат работу:
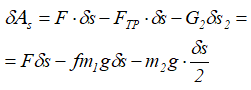
Обобщенная сила
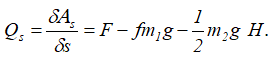
Обобщенная сила, соответствующая обобщенной координате φ, определится, если зададим φ малое приращение δφ (s — не меняется!)
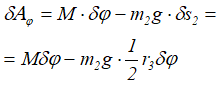
и посчитаем работу действующих сил
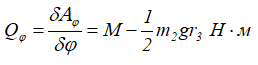
Далее: