Обобщенной силой Qi, соответствующей обобщенной координате qj, называют скалярную величину, определяемую отношением элементарной работы действующих сил на перемещении механической системы, вызванную изменением обобщенной координаты qj, к величине приращения этой координаты δqj:
или
Размерность обобщенной силы зависит от размерности обобщенной координаты и может выражаться в единицах силы [Н], момента [Н∙м]. Число обобщенных сил для данной системы соответствует числу обобщенных координат.
При необходимости можно сосчитать обобщенные силы от внешних сил QiF, обобщенные силы реакций связей QiR, обобщенные силы от сил инерции QiΦ.
Радиус-вектор произвольной точки механической системы есть функция обобщенных координат:
поэтому приращение радиуса-вектора, вызванное изменением, например, обобщенной координаты qj, будет
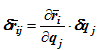
тогда работа приложенных к системе сил на малом перемещении будет
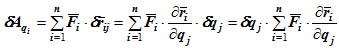
То есть обобщенная сила может быть выражена соотношением
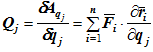
Расписав скалярное произведение, получим
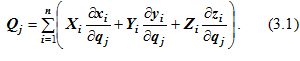
Для консервативной системы силы поля, действующие на точки механической системы, выражаются соотношениями
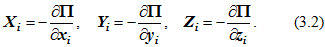
Учитывая, что радиус-вектор любой точки и потенциальная энергия системы есть функция координат и, следовательно, обобщенных координат, можно получить из выражения (3.1):
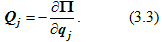
Далее: