Решение задачи (РГР) Д1 «Интегрирование дифференциальных уравнений движения материальной точки» по разделу «динамика» теоретической механики.

Пример определения уравнений движения точки в координатной форме для свободной материальной точки массой m движущейся под действием силы F.

Рассмотрим следующие случаи выражения силы, действующей на точку:

1. сила зависит от времени;
2. сила зависит от положения точки в пространстве;
3. сила зависит от скорости точки.

Задача

Пусть свободная материальная точка массой m движется под действием силы

Необходимо определить уравнения движения точки в координатной форме.

Решения других задач

Решение

Запишем для этой точки дифференциальные уравнения в проекциях на декартовы оси координат

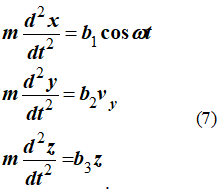
Первое уравнение системы (7) можно представить в виде двух уравнений первого порядка

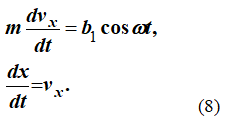
В первом уравнении связаны две переменные величины: проекция скорости на ось x и время. Разделяя переменные, получим

Слева и справа от знака равенства стоят дифференциалы некоторых функций.

Если дифференциалы равны, то и интегралы равны с точностью до постоянной интегрирования

После интегрирования получим

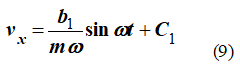
т.е. зависимость проекции скорости точки на ось x от времени. Из второго уравнения системы (8) получим

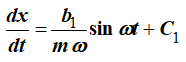
Снова, разделяя переменные, получим

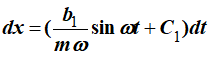
После интегрирования получим

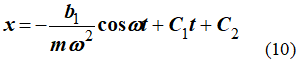
Постоянные C₁ и C₂ определим по начальным условиям. Подставляя в выражение (10) значение координаты x при t=0, получаем

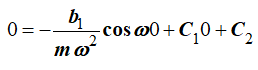
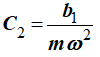
Постоянную C₁ определим, подставляя в (9) значение v_x при t=0:

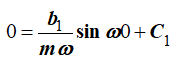
отсюда C₁=0.

Таким образом, решение первого уравнения системы (7) имеет вид

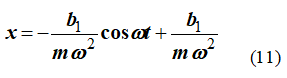
Второе уравнение системы (7) также представляем в виде двух уравнений

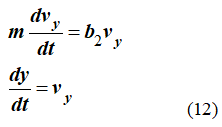
Разделяя переменные в первом уравнении, получим

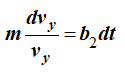
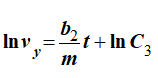
Решая относительно v_y, получим

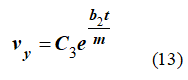
Учитывая второе уравнение системы (12) снова получаем

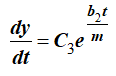
Разделяя переменные и интегрируя, получим

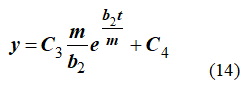
Постоянные C₃ и C₄ определяем по начальным условиям.

Из (13)

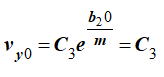
Из (14)

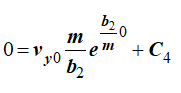
или

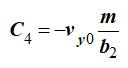
Таким образом, решение второго уравнения системы (7) имеет вид

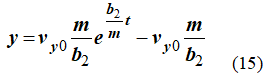
Третье уравнение системы (7) также представляем в виде двух уравнений

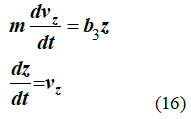
В первом уравнении системы (16), связаны три переменных величины: скорость, время и координата точки.

Чтобы разделить переменные необходимо исключить одну из них. Произведем замену

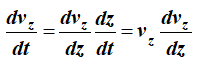
Тогда первое уравнение (16) примет вид

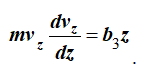
Теперь можно разделить переменные

Интегрируя, получим

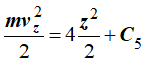
Решая относительно v_z, получим

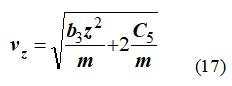
По начальным условиям найдем постоянную C₅.

Подставляя в (17) v_z0= 0 и z₀, получим

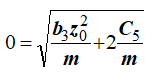
и

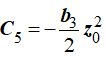
Учитывая, что

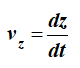
выражение (17) запишется в виде

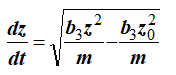
Разделив переменные, приведем его к виду

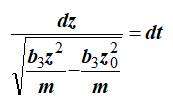
Вынося из под знака корня в знаменателе b₃/m, получим

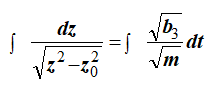
Интегрируем

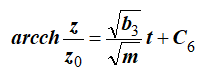
Решая относительно z получаем

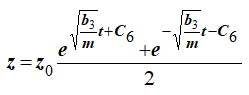
Постоянную C₆ найдем по начальным условиям.

При t=0, z₀≠0, отсюда

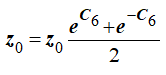
или

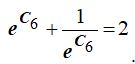
Решая относительно C₆, получим

или C₆=0.

Таким образом, решение третьего уравнения системы (7) будет иметь вид

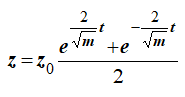
Окончательно уравнения движения точки в координатной форме имеют вид:

---

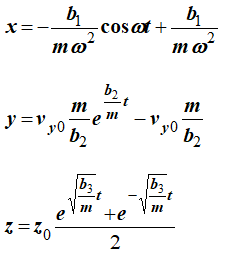
Далее: