Пример решения задачи по определению опорных реакций в глухой и бискользящей заделках и давления в шарнире составной конструкции, нагруженной равномерно распределенной нагрузкой с интенсивностью q, парой сил с моментом M и сосредоточенной силой F, расположенной под углом α.

Задача

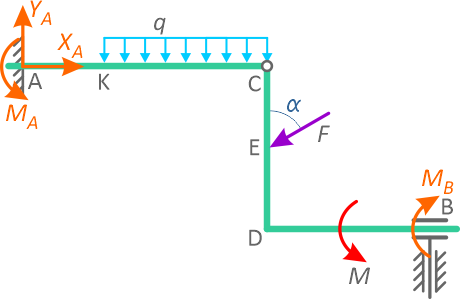
Две части системы соединены между собой шарниром в точке C (рисунок 2.8). В точке A – глухая заделка, в точке B – бискользящая заделка.

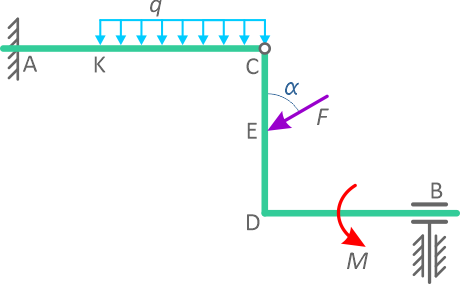
Конструкция нагружена равномерно распределенной нагрузкой с интенсивностью q=20 кН/м, парой сил с моментом M=30 кНм и сосредоточенной силой F=10 кН под углом α=60°.

Расстояния между характерными точками конструкции: AC=3м, CD=DB=KC=2м, AK=CE=ED=1м.

Требуется определить опорные реакции и давление на шарнир C.

Решение

Короткое видео про реакции в разных типах заделок:

Другие видео

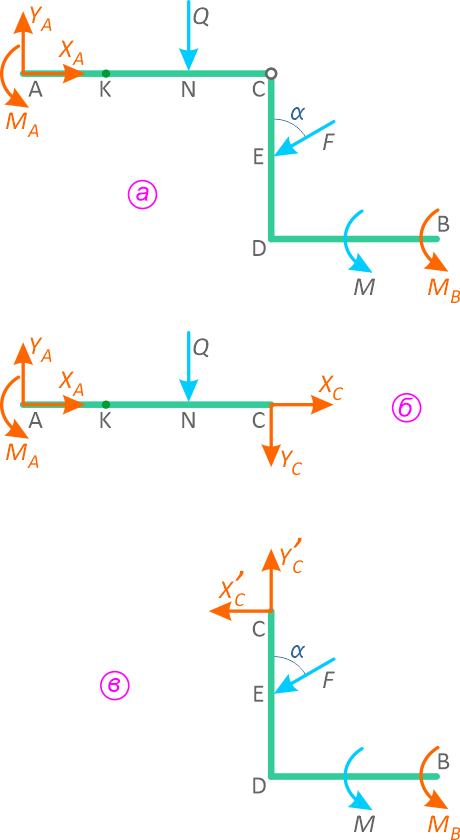
На рисунке 2.9 на освобожденной от связей системы (рисунок 2.9, а) и ее отдельных элементах (рисунок 2.9, б, в) показаны силы, действующие на всю конструкцию в целом и на две выделенные ее части.

Действие глухой заделки в точке A заменено силами X_A, Y_A и моментом M_A, в бискользящей заделке – моментом M_B. При разделении двух частей их действие друг на друга показано силами X_C, Y_C и X′_C, Y′_C причем

Для каждой из частей можно написать по три уравнения равновесия и найти с учетом (2.20) неизвестные опорные реакции X_A, Y_A, M_A, M_B и давление в шарнире C (X_C, Y_C).

Для удобства проведения расчетов распределенную нагрузку q заменим её равнодействующей Q=q×KC=20×2=40кН, которая приложена в середине участка KC в точке, которую обозначим буквой N.

Уравнения равновесия для левой части конструкции:

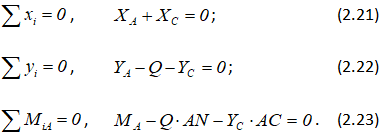
Для правой части:

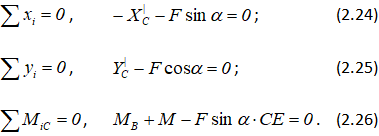
Из уравнений (2.21 – 2.26) находим неизвестные величины.

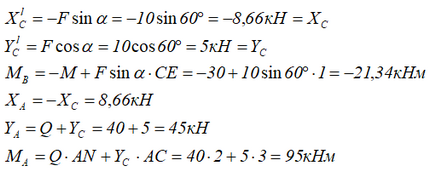
Систему уравнений равновесия можно составить иначе: например, написать три уравнения для системы в целом (рисунок 2.9, а) и три уравнения для какой-либо одной ее части.

В любом случае есть возможность получить три уравнения для проверки правильности решения. В данном расчете это уравнения для всей конструкции:

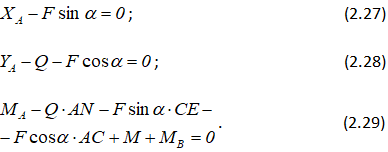
Подставив в них найденные из первых шести уравнений величины, можно проверить правильность решения.

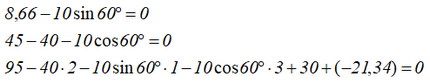
Покажем на схеме истинное направление опорных реакций в глухой и бискользящей заделках заданной шарнирной системы.

---

Далее: