Пример решения задачи по определению силы натяжения троса и опорной реакции в шарнирно-неподвижной опоре балки, удерживаемой тросом.

Задача

Однородная балка AB весом P закреплена в точке A шарнирно-неподвижной опорой; трос BC, удерживающий балку, составляет с ней угол α.

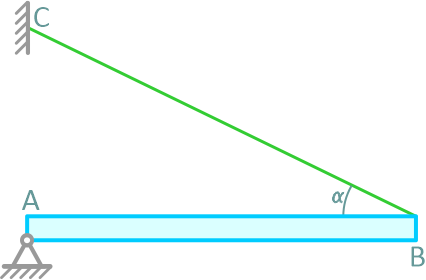
Определить натяжение троса и реакцию опоры A.

Другие примеры решений >
Помощь с решением задач >

Решение

Силы, действующие на балку, приложены к разным ее точкам, поэтому в данной задаче нужно рассмотреть равновесие балки. Балка однородная, поэтому сила P (вес балки) приложена к ее середине.

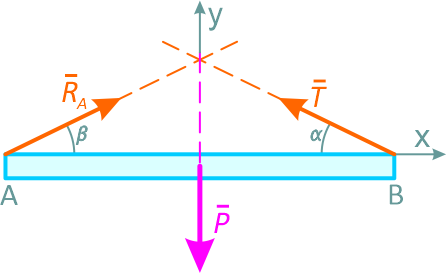
Реакция троса – сила T – направлена вдоль троса. Направление реакции опоры A можно определить, воспользовавшись теоремой о трех силах. По этой теореме линии действия трех непараллельных сил P, T и R_A должны пересекаться в одной точке. То есть угол β должен быть равен углу α.

Короткое видео про реакции в разных типах связей:

Другие видео

Далее возможно геометрическое или аналитическое решение.

Так как система находится в равновесии, то

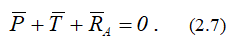
Строим это геометрическое равенство, начиная с известной силы P; под углом α к горизонтали через конец векторa P проводим линию MN, вдоль которой направлена сила T.

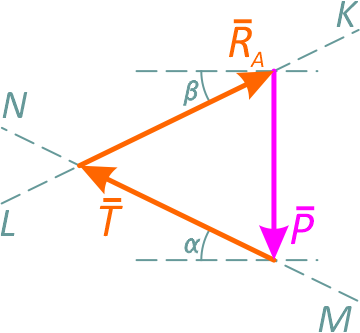
Так как сумма всех сил должна быть равна нулю, то вектор R_A должен заканчиваться в начале вектора P под углом β к горизонту (линия KL).

Точка пересечения линий MN и KL – это конец вектора T и начало вектора R_A. Далее можно определить величины T и R_A, умножив длины отрезков на выбранный масштаб или воспользовавшись теоремой синусов:

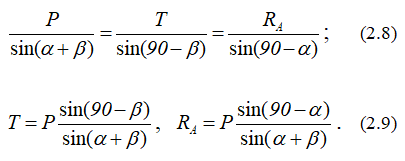
Аналитическое решение предполагает составление двух уравнений. Проецируем векторное равенство (2.7) на выбранные оси координат и получаем два уравнения равновесия с двумя неизвестными:

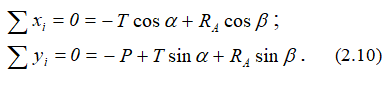
Из этих уравнений определяются величины T и R_A:

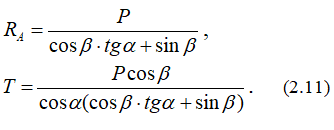
Остается только подставить значения и выполнить окончательный расчет величины искомых сил.

Другие примеры решения задач >>