Пример решения задачи по теме «сложное движение точки» теоретической механики, определение в заданный момент времени абсолютной скорости и абсолютного ускорения точки, движущейся по ободу диска, вращающегося вокруг оси.

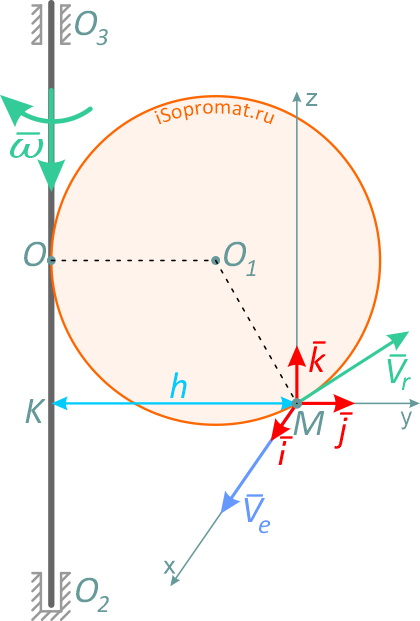
Задача

Диск радиуса R=0,5 м вращается вокруг оси, лежащей в его плоскости и касающейся диска, с угловой скоростью ω = πt² c^-1 (рисунок 1). По ободу диска движется точка M по закону: ∪OM = πRt²/6 м.

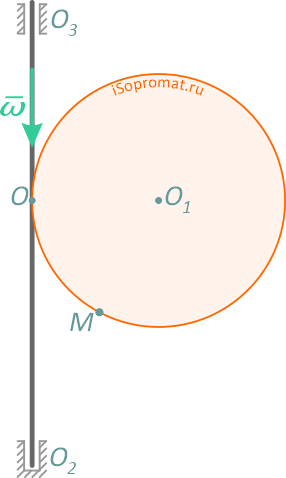
Требуется, в момент времени t=2 cекунды, определить абсолютные скорость и ускорение точки M.

Решение

Точка M в данном примере совершает сложное движение, которое может быть разложено на два движения: относительное движение — движение точки M по движущемуся диску (именно с ним может быть скреплена подвижная система отсчета) и переносное движение — вращение диска вместе с находящейся на нем точкой.

Поскольку переносное движение по определению это движение той точки диска, в которой находится в данный момент точка M, то сначала необходимо определить положение точки M на диске в момент времени t=2 c:

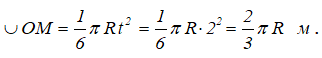
Центральный угол составит

Расчет скорости

В относительном движении закон движения задан естественным способом, поэтому скорость определяется как производная его дуговой координаты и направлена по касательной к траектории относительного движения в плоскости диска:

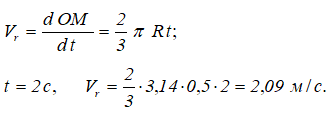
Переносное движение в данном случае — вращение вокруг неподвижной оси O₂O₃, расстояние до которой от точки M равно KM.

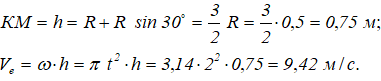
По направлению вектора угловой скорости ω определяем, что при вращении вокруг оси O₂O₃ точка M движется к нам, то есть вектор V_e перпендикулярен плоскости диска и для выбранной системы отсчета Mxyz, скрепленной с диском, направлен по оси Mx.

Абсолютная скорость точки в нашем примере определяется как геометрическая сумма векторов:

численная величина:

Спроецировав векторную сумму на выбранные оси координат, получим проекции абсолютной скорости на эти оси:

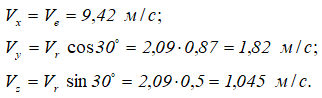
Направление вектора скорости определяют направляющие косинусы, то есть углы, которые вектор скорости составляет с выбранными осями:

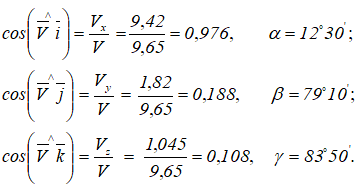
Расчет ускорения

В данном примере и переносные и относительные движения точки M — криволинейные, поэтому абсолютное ускорение определяется по формуле:

Составляющие ускорения определяются независимо друг от друга. В переносном движении точка M вращается вокруг оси O₂O₃ и движется по окружности радиуса h (рисунок 3).

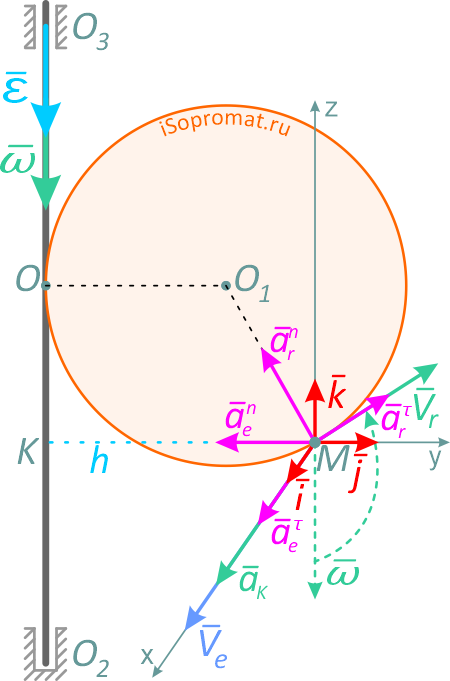
Нормальное ускорение в этом движении:

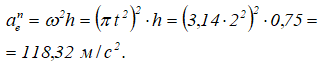
Этот вектор направлен от точки M к точке K (к оси вращения).

Касательное ускорение в переносном движении определится по формуле

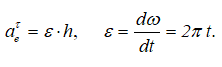
Знак производной положителен, то есть вращение ускоренное и направления векторов V_e и a_e^τ совпадают:

В относительном движении точка M движется по окружности радиуса R. Нормальное ускорение:

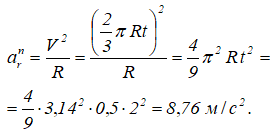
Этот вектор направлен от точки M к центру окружности — точке O₁.

Касательное ускорение в относительном движении:

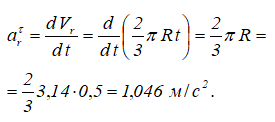
Производная от относительной скорости получена со знаком плюс, поэтому a_e^τ совпадает по направлению с V_r.

Кориолисово ускорение определяется по формуле

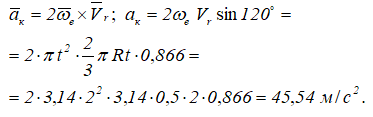
Вектор кориолисова ускорения должен быть перпендикулярен векторам ω_e и V_r (в нашем случае перпендикулярен плоскости чертежа). Если смотреть навстречу вектору a_k, то мы должны видеть поворот вектора ω_e (мысленно перенесенного в точку) на кратчайший угол до совмещения с вектором V_r, происходящий против хода часовой стрелки. То есть в этом примере вектор a_k направлен по оси Mx к нам.

Направление кориолисова ускорения может быть определено и по правилу Жуковского.

Проецируем вектор V на плоскость, перпендикулярную вектору ω_e (на плоскость Mxy; в данном примере эта проекция совпадает с осью My), и поворачиваем проекцию V_r на 90° в сторону вращения, то есть вектор a_k направлен к нам по оси Mx.

Для определения абсолютного ускорения проецируем векторное равенство (3.6) на оси координат:

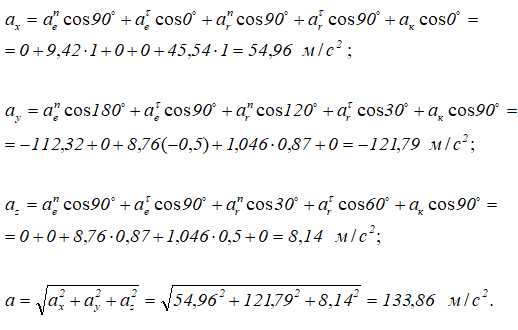
Направление вектора ускорения определяется с помощью направляющих косинусов (см. формулы (3.7)):

---

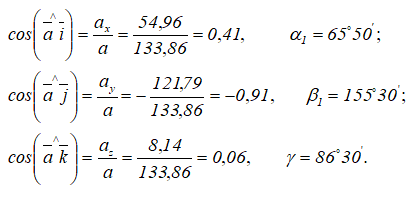
Далее: