Фермой называется шарнирно-стержневая система, элементами которой являются стержни, шарнирно скрепленные между собой по концам.

Точки соединения стержней в любой стержневой системе называются узлами.

Фермы применяются для перекрытия значительных пролетов там, где применение обычных балок становится экономически невыгодным.

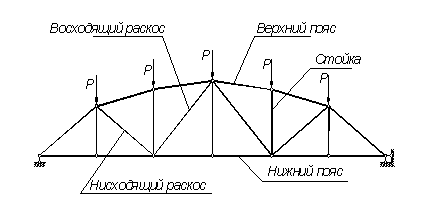
Рисунок 2.17 – Основные элементы фермы

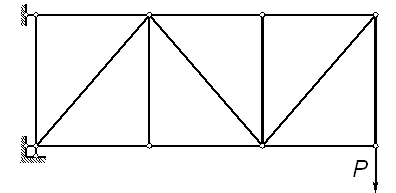
Рисунок 2.18 – Консольная ферма

В используемых на практике строительства фермах, стержни соединены между собой, как правило, не шарнирно, а жестко. Однако к ним применима с достаточной степенью приближения шарнирно-стержневая расчетная схема.

Действительно, в реальных фермах стержни искривляются очень слабо, а их изгибная жесткость очень мала, поэтому возникающие в стержнях изгибающие моменты пренебрежительно малы по сравнению с продольная сила, и стержни работают как шарнирно-закрепленные.

Применимость шарнирно-стержневой схемы к реальным фермам подтверждена экспериментальной и расчетной практикой.

В фермах, применяемых для покрытий, перекрытий и мостов следует различать: верхний и нижний пояса, а также решетку (рисунок 2.17).

Решетка состоит из наклонных (восходящих − повышающихся к середине пролета и нисходящих) раскосов и вертикальных стоек (последние могут отсутствовать).

Фермы по длине пролета делятся на панели, обычно ограниченные соседними узлами поясов.

В однопролетной ферме, нагруженной действующей вниз нагрузкой — верхний пояс сжат, а нижний растянут; нисходящие раскосы вблизи опор фермы растянуты, а верхние сжаты. Стойки решетки при нагрузке по верхнему поясу сжаты, а при нагрузке по нижнему поясу — растянуты.

В консольных фермах (рисунок 2.18) верхний пояс растянут, а нижний сжат.

Расчет ферм обычно производится при узловой передаче нагрузки.

Как правило, любая нагрузка может быть приведена к узловой посредством специальных устройств перераспределения (рисунок 2.19).

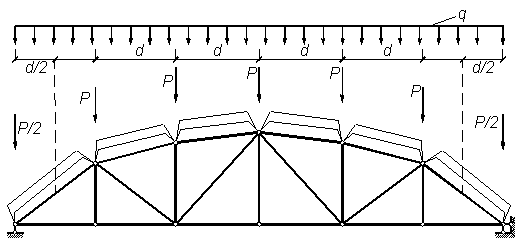
Рисунок 2.19 – Пример перехода от равномерно распределенной нагрузки к узловой

q = q_const×a,

где а – шаг ферм;

P = q×a×d,

где d – длина панели

Известно, что при узловой передаче нагрузки в стержнях фермы возникают только продольные усилия (это возможно лишь в том случае, если оси сходящихся стержней центрированы в узлах, а также при отсутствии трения в шарнирах узлов).

Напомним, что проектировочный и проверочный расчет сечений элементов фермы проводится по известной из курса сопротивления материалов формуле (условие прочности при растяжении (сжатии)):

σ = N / А ≤ R

где N — возникающее в сечении одного из элементов продольное усилие;

А — площадь поперечного сечения элемента;

R — расчетное сопротивление материала на растяжение (сжатие), регламентируемое соответствующим СНиП ("Строительные нормы и правила").

Для сжатых элементов необходимо произвести дополнительную проверку на возможную потерю устойчивости:

σ = N / А < φ× R

где φ — коэффициент продольного изгиба.

На основе изложенного, возникает необходимость принятия следующих допущений:

• связи ферм считаются идеальными, то есть в шарнирах узлов фермы отсутствует трение;
• оси сходящихся стержней центрированы в узлах.

Классификация ферм

Шарнирно-стержневые системы (фермы) различают по следующим признакам:

А. По очертанию внешнего контура:

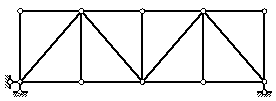
Рисунок 2.20 – С параллельными поясами

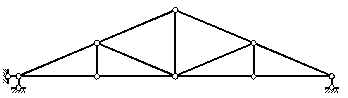
Рисунок 2.21 – Треугольного очертания

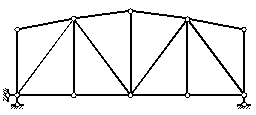
Рисунок 2.22 – Полигональные фермы

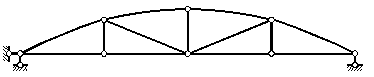
Рисунок 2.23 – С параболическим очертанием

Б. По типу решетки:

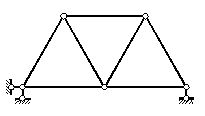
Рисунок 2.24 – С треугольной раскосной решеткой

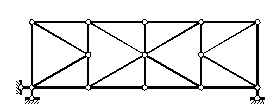
Рисунок 2.25 – С полураскосной решеткой

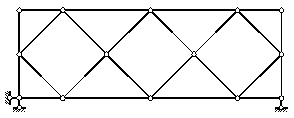
Рисунок 2.26 — С ромбической решеткой

В. По типу опирания:

1. балочные (рисунок 2.17);
2. консольные (рисунок 2.18);
3. консольно-балочные.

Г. По назначению:

1. стропильные;
2. крановые;
3. башенные;
4. мостовые

и другие.

Д. По количеству степеней свободы системы:

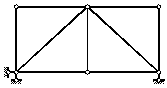
Рисунок 2.27 — Статически определимые, W=0

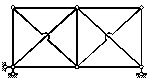
Рисунок 2.28 — Статически неопределимые, W<0

Кроме плоских ферм, у которых оси всех стержней расположены в одной плоскости, применяются также пространственные фермы, оси элементов которых не лежат в одной плоскости.

Расчет пространственной фермы во многих случаях удается свести к расчету нескольких плоских ферм.

Расчет статически определимых систем >
Примеры решения задач >