Примеры решения задач по определению коэффициента трения скольжения f между лестницей прислоненной к стене и шероховатой горизонтальной поверхностью (полом), при котором она, опираясь верхним концом о гладкую стену, будет находиться в состоянии статического равновесия или начнет скользить.

Определение коэффициента трения лестницы прислоненной к стене

Задача 1

Приставная лестница прислонена к стене под углом α и упирается в пол.

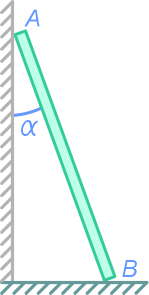
Требуется определить, при каком минимальном коэффициенте трения между полом и лестницей последняя может находиться в равновесии, опираясь верхним концом о гладкую стену.

Вес лестницы G=120 Н, угол между лестницей и стеной α=20°

Решение

На лестницу действует только одна нагрузка – ее собственный вес, приложенный в точке C посередине длины лестницы AB.

Вес лестницы уравновешен реакцией R_A гладкой стены и реакцией шероховатого пола, которую заменим двумя составляющими: R_n – нормальной составляющей и F_ТР – силой трения.

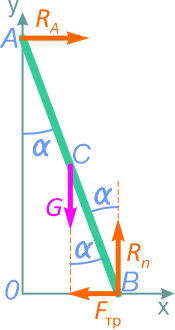
В данном случае, реакция R_A будет направлена по нормали к соприкасаемой поверхности.

Составим три уравнения равновесия:

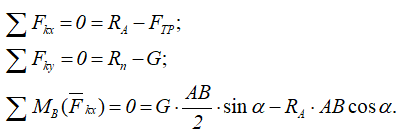
Откуда получаем

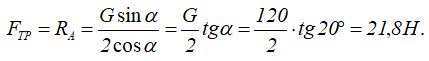
Отсюда минимальный коэффициент трения, обеспечивающий равновесие лестницы определяем по формуле

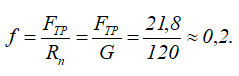
Таким образом, лестница будет находиться в равновесии при всех значениях f ≥ 0,2.

Расчет коэффициента трения скольжения балки опирающейся на выступ

Задача 2

Однородная балка весом P и длиной l опирается на шероховатую поверхность и выступ высотой h.

Коэффициент трения балки о пол равен f, угол наклона балки к полу равен α.

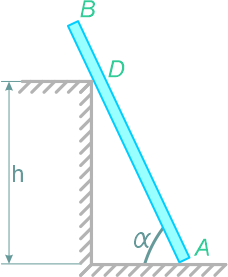
Дано: P=250 Н, l=8 м, h=5 м, α=60°.

Требуется найти коэффициент трения f, при котором балка начнет скользить.

Решение

Здесь, реакция R_D будет направлена по нормали к соприкасаемой поверхности.

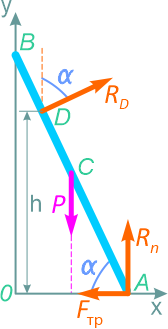
Аналогично предыдущей задаче записываем три уравнения равновесия системы:

Две суммы проекций всех сил на оси x и y, и суммы моментов относительно нижней точки балки.

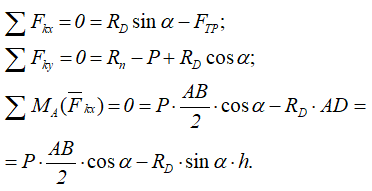
Из полученных уравнений выражаем и определяем значения составляющих реакций связей

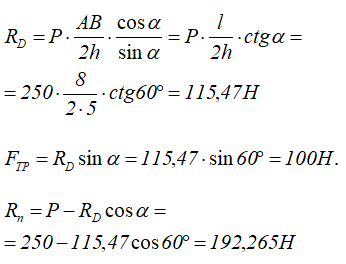
Искомый коэффициент трения f определим из отношения силы трения скольжения к нормальной реакции в точке.

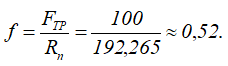
Ответ: для того чтобы балка начала скользить, коэффициент трения скольжения не должен превышать значение f < 0,52

---

Далее: