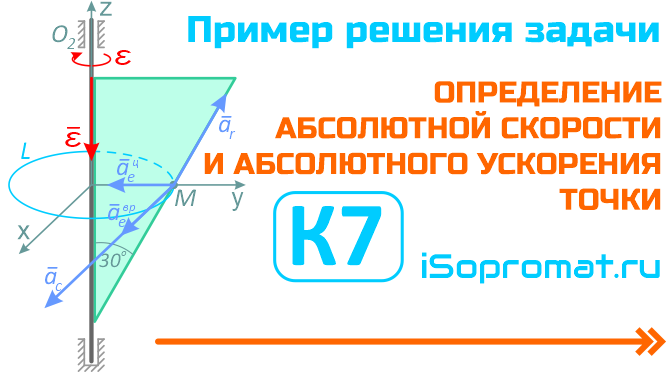
Решение задачи (РГР) К7 «Определение абсолютной скорости и абсолютного ускорения точки» по разделу «кинематика» теоретической механики.

Пример определения для заданного момента времени абсолютной скорости и абсолютного ускорения точки при сложном движении по заданным уравнениям относительного движения точки и треугольника, вращающегося вокруг оси.

Задача

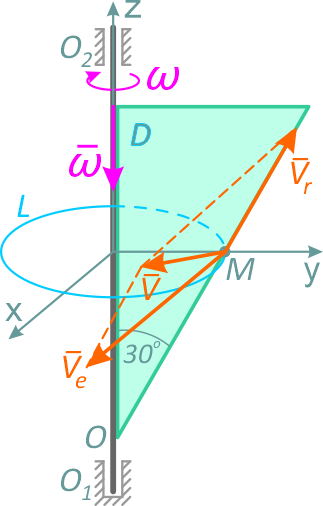
Треугольник D вращается вокруг оси O₁O₂ (рис. 1, а). По наклонной стороне треугольника движется точка M.

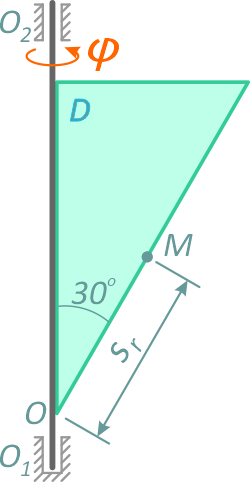
Требуется, по заданным уравнениям относительного движения точки M и движения треугольника D определить для момента времени t=t₁ абсолютную скорость и абсолютное ускорение точки M.

Дано:

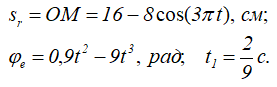
Решение

Точка M совершает сложное движение — движется относительно треугольника D и вместе с треугольником вращается вокруг оси O₁O₂.

Тогда движение точки относительно треугольника будет относительным, движение вместе с треугольником – переносным.

Будем считать, что в заданный момент времени плоскость чертежа совпадает с плоскостью треугольника D. Положение точки M на треугольнике D определяется расстоянием s_r = OM.

При

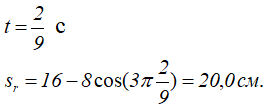
Абсолютную скорость точки М найдем как геометрическую сумму относительной и переносной скоростей:

Модуль относительной скорости

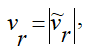
где

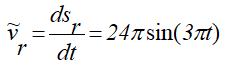
— алгебраическое значение относительной скорости.

При

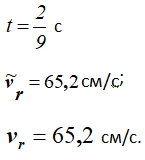
Положительный знак у v_r показывает, что вектор v_r направлен в сторону возрастания s_r.

Модуль переносной скорости

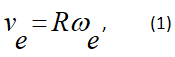
где R – радиус окружности L, описываемой той точкой тела, с которой в данный момент совпадает точка М;
R = s_rsin30° = 10,0 см;
ω_e – модуль угловой скорости тела

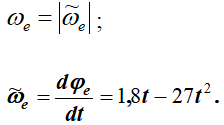
При

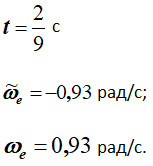
Отрицательный знак у величины ω_e показывает, что вращение треугольника происходит вокруг оси Oz в сторону, обратную направлению отсчета угла φ. Поэтому вектор ω_e направлен по оси Oz вниз (рис. 1, б).

Модуль переносной скорости определяется по формуле (1)

Вектор v_e направлен по касательной к окружности L в сторону вращения тела.

Так как v_e и v_r взаимно перпендикулярны, модуль абсолютной скорости точки М

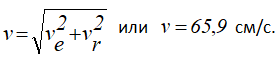
Абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений

или в развернутом виде

Модуль относительного касательного ускорения

где

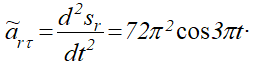
При

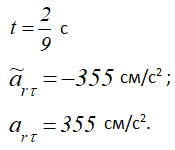
Отрицательный знак a_rτ показывает, что вектор a_rτ направлен в сторону отрицательных значений s_r. Знаки v_r и a_rτ различны, следовательно, относительное движение точки М замедленное.

Относительное нормальное ускорение

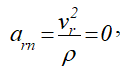
так как траектория относительного движения – прямая (ρ = ∞).

Модуль переносного вращательного ускорения

где

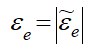
– модуль углового ускорения тела D

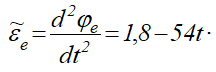
При

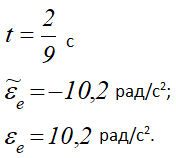
Знаки ε_е и ω_e одинаковы; следовательно, вращение треугольника D ускоренное, направления векторов ε_е и ω_e совпадают (рис. 1, б, в).

Согласно (2) a_e^в = 102 см/с². Вектор a_e^в направлен в ту же сторону, что и вектор v_e.

Модуль переносного центростремительного ускорения

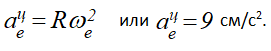
Вектор a^ц_e направлен к центру окружности L.

Кориолисово ускорение

Модуль кориолисова ускорения

где

С учетом найденных выше значений ω_e и v_r получаем

Вектор a_C направлен, согласно правилу векторного произведения, к нам — перпендикулярно плоскости треугольника D (рис. 1, в).

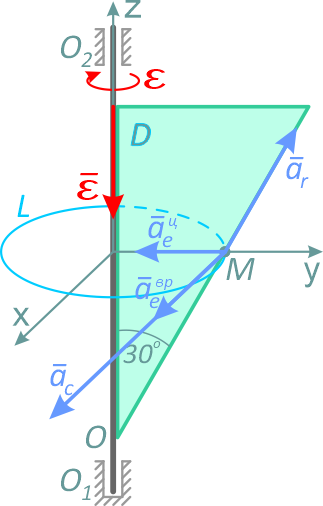
Модуль абсолютного ускорения точки М находим способом проекций:

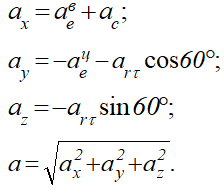
Результаты расчета сведены в таблицу 1.

---

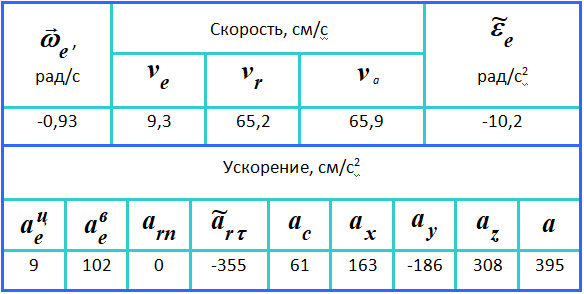
Далее: