Задание к РГР С7 «Определение реакций опор твердого тела» по теоретической механике с примерами решения.
- Введение
- Краткие сведения из статики твердого тела
- Примеры выполнения задания
- Задание для самостоятельной работы
- Рекомендуемая литература
- Вопросы для самоконтроля
Введение
Целью учебно-методического пособия по выполнению расчетно-графической работы «Определение реакций опор твердого тела» является оказание методической помощи студентам, изучающим раздел «Статика твердого тела» в дисциплине «Теоретическая механика».
Прикладные задачи этой темы применимы и в других разделах курса, а также в дисциплинах «Сопротивление материалов», «Детали машин» и в ряде специальных дисциплин.
Номер варианта чертежа и исходных данных соответствует порядковому номеру студента в списке группы.
Задание для самостоятельной работы
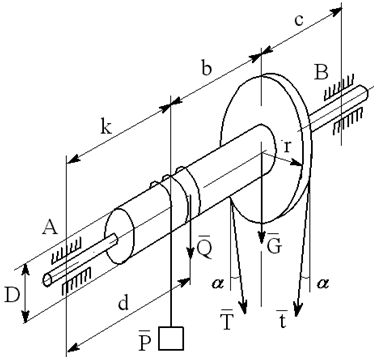
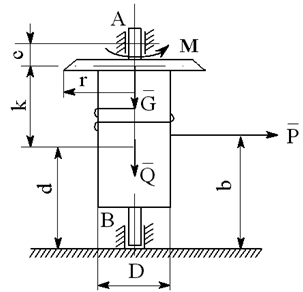
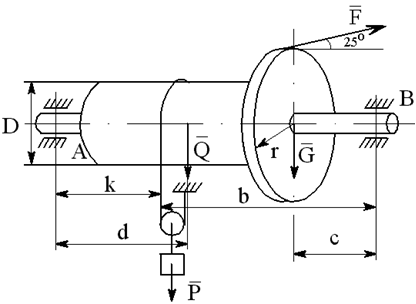
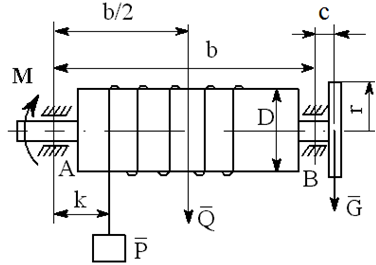
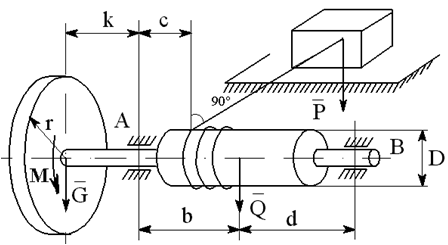
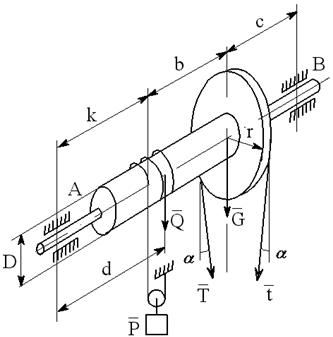
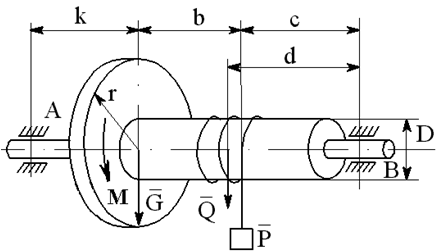
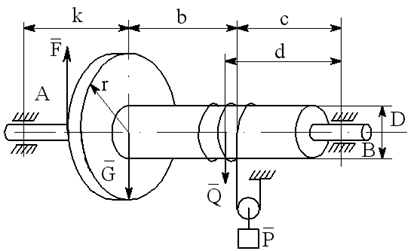
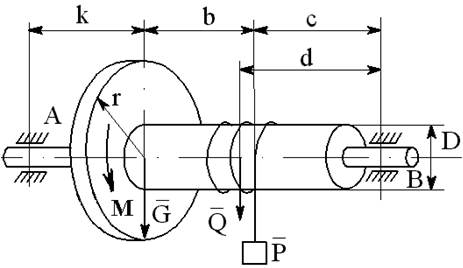
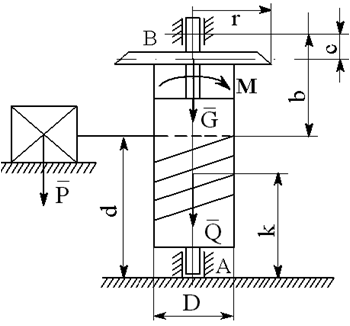
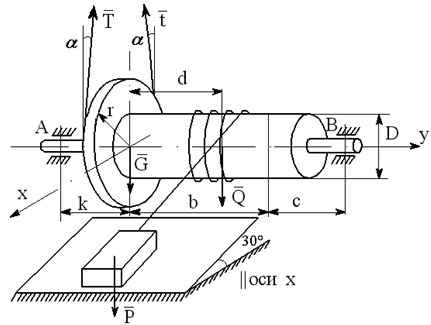
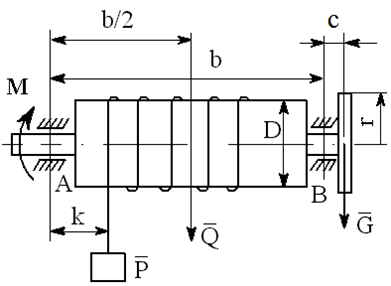
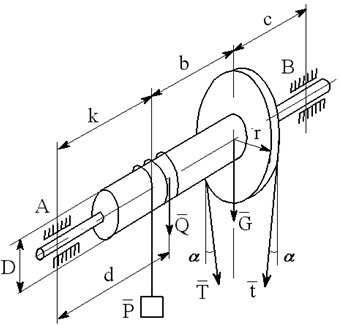
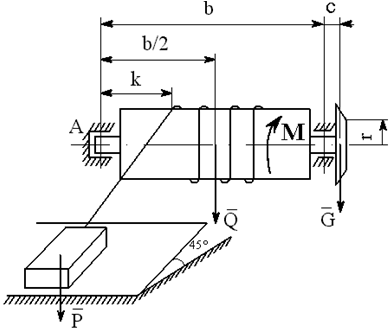
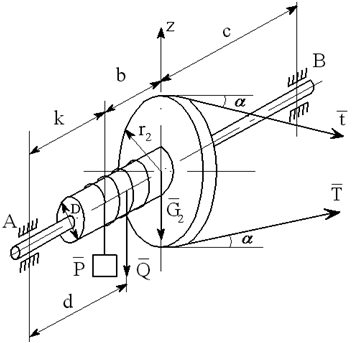
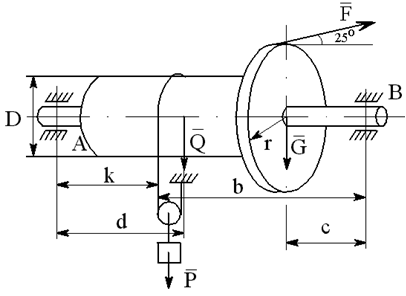
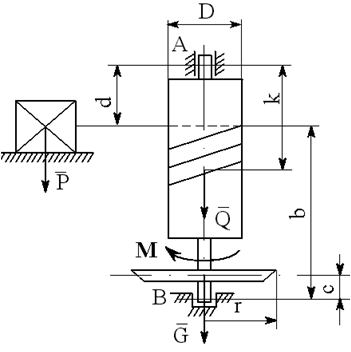
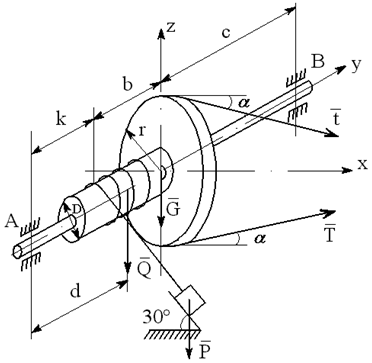
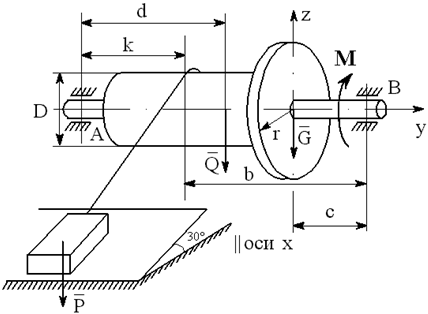
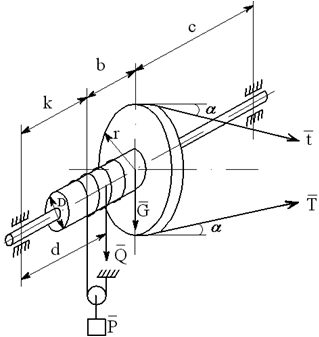
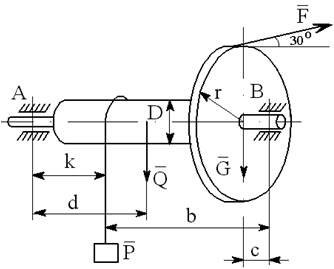
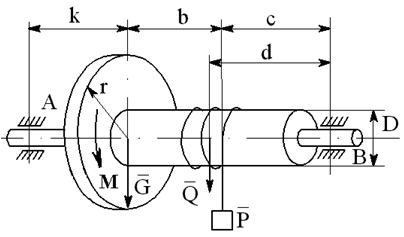
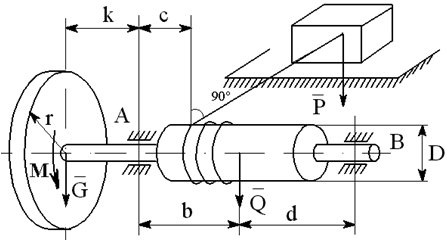
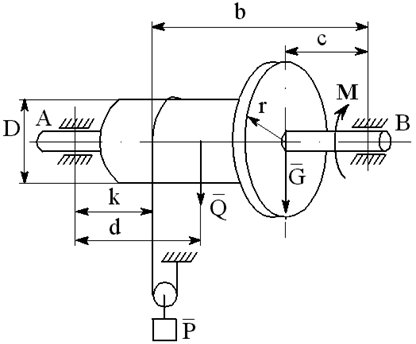
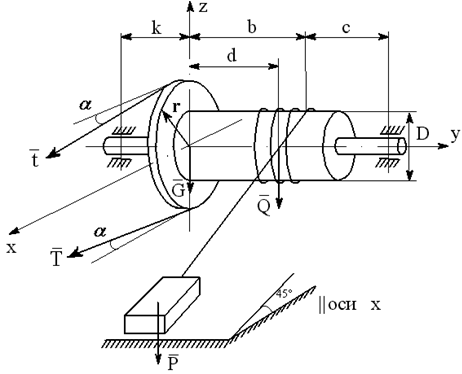
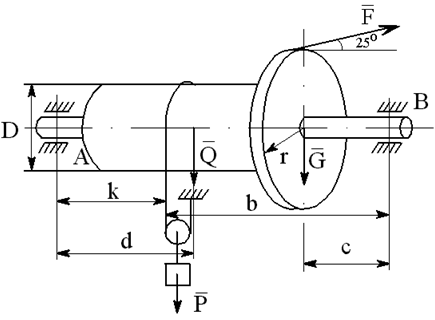
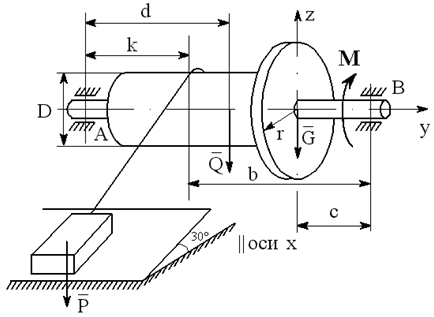
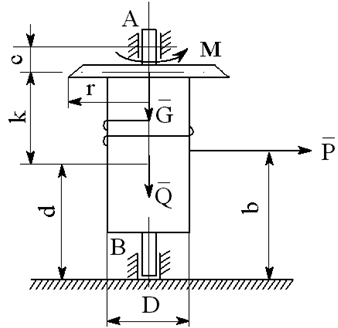
На вал с барабаном весом Q намотана веревка, удерживающая груз весом P , и насажено колесо радиусом r и весом G.
Определить реакции подшипников A и B и силу F , приложенную к колесу в плоскости его вращения, или момент M, приложенный к валу (варианты №2-6, 8-11, 13, 15, 17-19, 21, 23-26, 28-30), или натяжение ремней, надетых на колесо (варианты №1, 7, 12, 14, 16, 20, 27; скольжение ремня отсутствует, T=2t), в случае равновесия конструкции. Коэффициент трения f=0,3 (варианты №6, 11, 12, 15, 17, 19-21, 25, 27, 29).
Варианты конструкций с размерами приведены на рисунках 1-30. Числовые значения величин приведены в таблице 3.1.
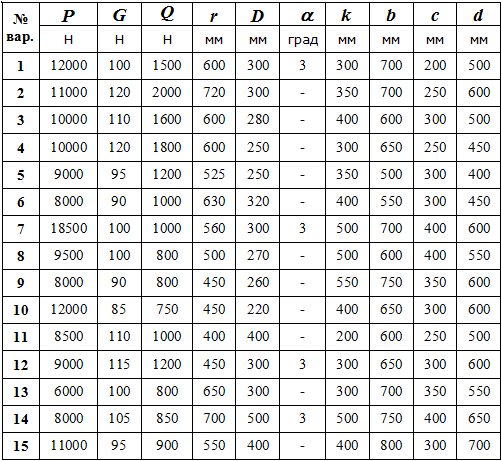
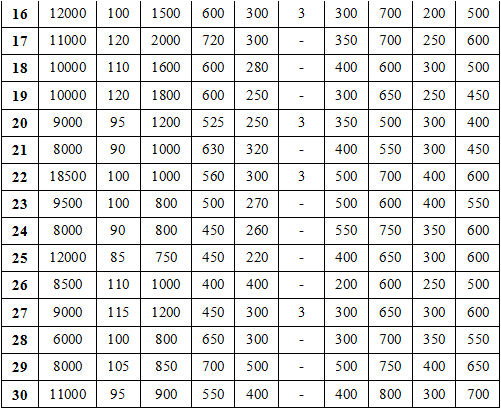
Варианты конструкций с размерами
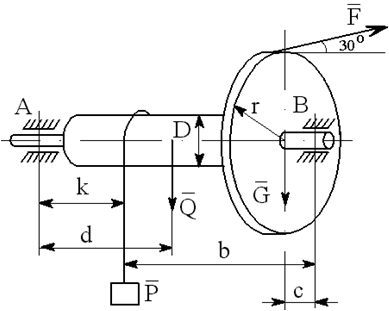

Рекомендуемая литература
- Яблонский А.А., Никифорова В.М. Курс теоретической механики. – СПб.: Лань, 1998. – 768 с.
- Айзенберг Т.Б. и др. Руководство к решению задач по теоретической механике / под ред. Воронкова И.М. – М.: Высшая школа, 1968. – 419 с.
- Сорокин В.Н. Краткий курс теоретической механики: в теории, задачах и плакатах: учебник /УГНТУ. – М.: Интер, 2005. – 600 с.
- Лекционный материал.
Вопросы для самоконтроля
- Как направлен и чему равен по модулю вектор-момент силы относительно данной точки?
- В каком случае вектор-момент силы относительно точки равен нулю?
- Что называется моментом силы относительно данной оси и как выбирается знак этого момента?
- В каких случаях момент силы относительно данной оси равен нулю?
- Какая существует зависимость между вектором-моментом силы относительно данной точки и моментом той же силы относительно оси, проходящей через эту точку?
- Что называется главным вектором произвольной пространственной системы сил?
- Что называется главным моментом произвольной пространственной системы сил?
- Каковы возможные случаи приведения произвольно расположенных и параллельных сил в пространстве?
- Каковы геометрическое и аналитическое условия приведения пространственной системы сил к равнодействующей?
- Сформулируйте теорему о моменте равнодействующей пространственной системы сил относительно точки и оси.
Далее: