Пример решения задачи по определению опорных реакций в подшипниках вала и силы натяжения ремня ременной передачи при заданных условиях.
Задача
При включении электродвигателя K груз Q весом 20 кН равномерно поднимается вверх (рисунок 2.12).
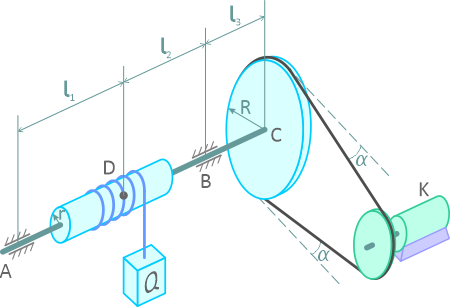
Требуется определить реакции в подшипниках A и B и натяжение бесконечного ремня, если считать, что натяжение ведущей его части в два раза больше натяжения ведомой (T1=2T2); α=30°; заданы расстояния l1, l2, l3; радиусы шкива – R и вала – r.
Решение
В задаче нужно рассмотреть пространственное равновесие ворота, к которому приложены внешние силы Q, T1, T2 и реакции опор YA, ZA, YB, ZB.
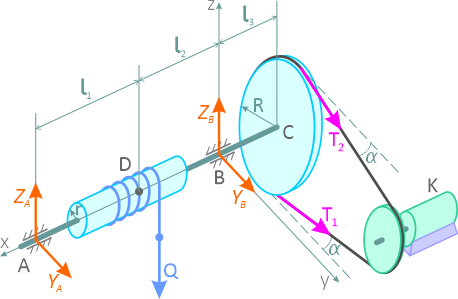
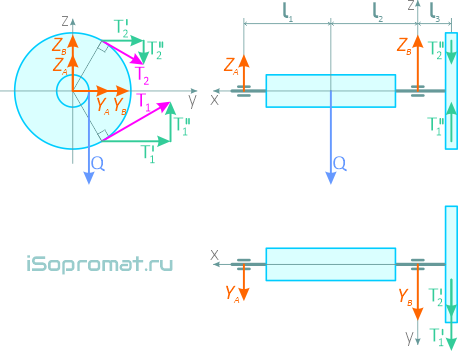
Прежде чем составлять уравнения равновесия, можно сделать дополнительные рисунки: вид навстречу каждой из координатных осей (фронтальную, профильную и горизонтальную проекции) (рисунок 2.13), которые помогут в составлении уравнений.
Составляем уравнения равновесия вала — три суммы проекций всех сил на оси x, y и z и три суммы моментов сил относительно этих же осей:
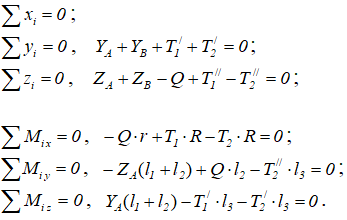
В этих уравнениях
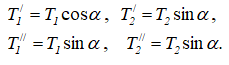
На ось x силы не проецируются. Поэтому из пяти уравнений находятся четыре неизвестные реакции: YA, ZA, YB, ZB и с учетом T1=2T2 находятся натяжения ремней T1 и T2.
Далее: