Рассмотрим порядок расчета плоского рычажного механизма с выходным звеном, совершающим вращательное движение.
Особенностью групп Ассура II класса 1-го и 2-го видов является то, что с геометрической точки зрения они имеют два решения. Поэтому применение общего принципа составления аналитических уравнений, изложенного выше, приводит к решению сложных квадратных уравнений, имеющих два корня.
Другие примеры решений >
Помощь с решением задач >
Возникает новая задача по выявлению того корня, который соответствует заданному механизму. Для упрощения решения задачи надо воспользоваться следующими рекомендациями:
- в группе 1-го вида при составлении векторного многоугольника необходимо «двигаться» от одного крайнего шарнира к другому, а не по звеньям группы;
- в группе 2-го вида при составлении суммы проекций необходимо провести вспомогательную ось перпендикулярно направляющей, по которой движется ползун, и рассмотреть построенный векторный многоугольник в проекции на эту ось.
Изображенный на рисунке 7 механизм содержит оба эти случая. При формировании векторного многоугольника для первой части этого механизма, включающей группу Ассура второго класса первого вида, проведен вектор AC, соединяющий крайние шарниры A и C данной группы (рисунок 7,б).
В результате определяются угол γ и размер AC, после чего в треугольнике ABC становятся известными все три стороны. По теореме косинусов можно определить любой из углов этого треугольника. В данном случае определяется угол α (рисунок 7,в), т.к. для дальнейшего решения задачи необходимо знать угол φ2.
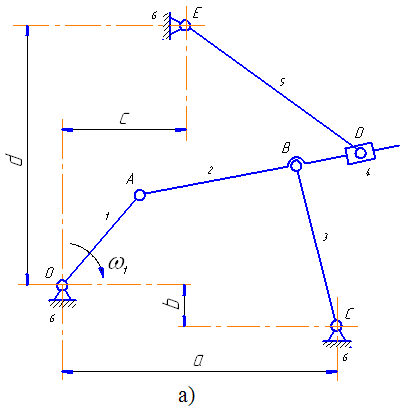
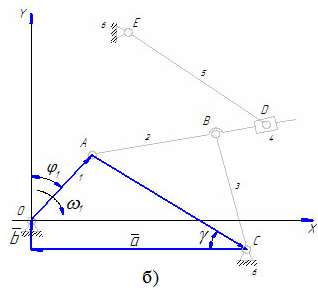
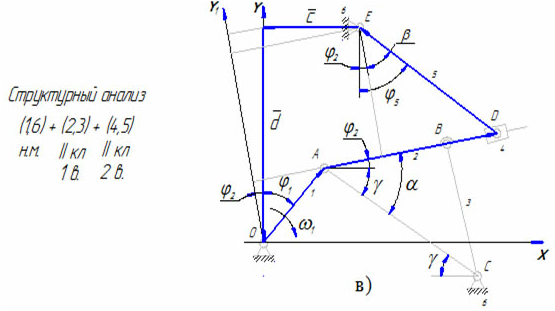
Рисунок 7 – Механизм с группами Ассура II класса 1-го и 2-го видов
Векторный многоугольник, включающий группу второго класса второго вида, рассматривается в проекции на ось Y1, проведенной перпендикулярно направляющей ABD (рисунок 7в). Полученное алгебраическое уравнение позволяет определить угол β и далее искомый угол φ5.
Конкретно аналитическое определение углового перемещения выходного звена 5, представленного на рисунке 7 (с учетом изложенных выше рекомендаций), будет иметь следующий вид:
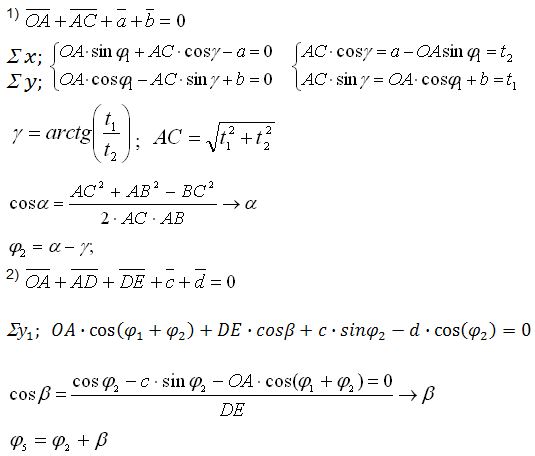
По этим уравнениям с помощью ЭВМ определяется угловое перемещение выходного звена φ5 в рад, угловая скорость ω5 в рад/с, угловое ускорение ε5 в рад/с2 для n положений механизма (в соответствии с заданием курсового проекта – для 24 положений).
Определение сил и моментов сил инерции >
Курсовой проект по ТММ >
