Сложное движение точки – это движение, при котором она одновременно движется относительно двух и более систем отсчета.
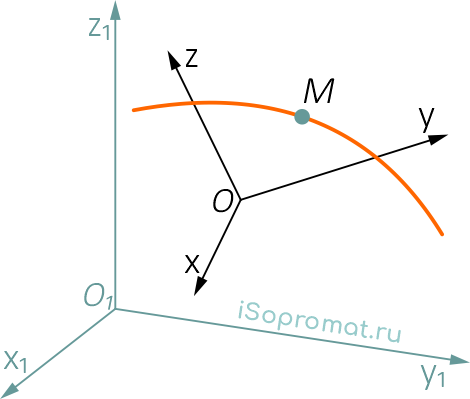
Рисунок 1
Законы Ньютона сформулированы для движения точки по отношению к инерциальным системам отсчета. Для определения кинематических параметров точки при движении относительно произвольно движущейся системы отсчета вводится теория сложного движения.
На рисунке 1 показаны:
- условно принимаемая за неподвижную система отсчета O1x1y1z1;
- движущаяся относительно неподвижной система отсчета Oxyz;
- точка M, перемещающаяся по отношению к подвижной системе отсчета.
Движение точки M в данном случае является сложным. Её движение по отношению к подвижной системе отсчета называют относительным движением.
Движение той точки подвижной системы отсчета, в которой в данный момент находится движущаяся точка, по отношению к неподвижной системе отсчета называют переносным движением. Движение точки M по отношению к неподвижной системе отсчета называют абсолютным движением.
По аналогии с этими определениями будут называться относительные, переносные и абсолютные скорости и ускорения точки.
Для их обозначения в относительном движении часто всего используется индекс r (relative – относительный) — Vr, ar; в переносном движении индекс e (entrained — увлекать за собой) — Ve, ae.
Ниже приведен пример сложного движения точки — M.
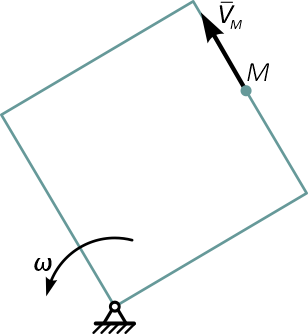
Рисунок 2
На рисунке 2 показан квадрат, вращающийся в плоскости чертежа вокруг неподвижной точки. По стороне квадрата движется точка M.
Она участвует в двух движениях, поэтому можно ввести две системы отсчета: неподвижную, например, O1x1y1z1 — по отношению к которой вращается квадрат и подвижную Oxyz, скрепленную с квадратом, по оси Oy которой движется точка M (рисунок 3).
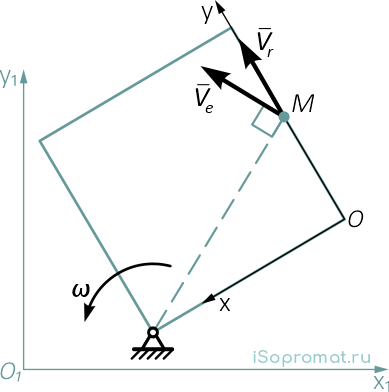
Рисунок 3
Движение точки M по стороне квадрата (по оси Oy скрепленной с квадратом подвижной системы) является относительным — скорость в этом движении Vr.
Вращение точки M вместе с квадратом — переносное движение, скорость в этом движении — Ve. Абсолютное движение является результатом сложения переносного и относительного движений.
Далее: