Аналитический метод кинематического исследования механизмов представляет звенья механизма, его характерные размеры и перемещения звеньев в виде векторов.
В результате формируются векторные многоугольники, на основании которых составляются векторные уравнения.
Рассматривая эти векторные уравнения в проекциях на оси произвольно выбранной системы координат, получают системы алгебраических уравнений, решая которые выводят уравнения для определения перемещений (линейных или угловых) исследуемых звеньев.
В качестве параметра выступает обобщенная координата начального звена (обычно угол поворота входного кривошипа).
Задавая различные значения обобщенной координаты, по полученным уравнениям определяют положения исследуемых звеньев в различных положениях механизма. Двойным дифференцированием уравнений перемещений получают уравнения для определения скоростей (линейных или угловых) и ускорений (линейных или угловых) исследуемых звеньев.
Однако, как показывает практика, уравнения скоростей и ускорений даже для простых механизмов получаются весьма громоздкими, с большой вероятностью получения ошибок при многоступенчатом дифференцировании.
Кроме того такой подход требует отдельного программирования для каждого механизма при использовании ЭВМ. Поэтому (как было показано выше) удобно использовать аналитический метод в комбинации с графическим методом в качестве алгоритма машинного решения задачи. Такой подход делает решение задачи весьма рациональным.
Особенностью групп Ассура II класса 1-го и 2-го видов является то, что с геометрической точки зрения они имеют два решения. Поэтому применение общего принципа составления аналитических уравнений, изложенного выше, приводит к решению сложных квадратных уравнений, имеющих два корня.
Возникает новая задача по выявлению того корня, который соответствует заданному механизму. Для упрощения решения задачи надо воспользоваться следующими рекомендациями:
- в группе 1-го вида при составлении векторного многоугольника необходимо «двигаться» от одного крайнего шарнира к другому, а не по звеньям группы;
- в группе 2-го вида при составлении суммы проекций необходимо провести вспомогательную ось перпендикулярно направляющей, по которой движется ползун, и рассмотреть построенный векторный многоугольник в проекции на эту ось.
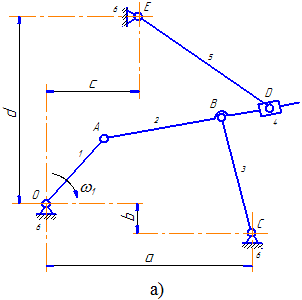
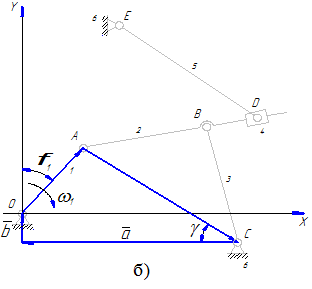
Изображенный на рисунке 11 механизм содержит оба эти случая. При формировании векторного многоугольника для первой части этого механизма, включающей группу Ассура второго класса первого вида, проведен вектор AC, соединяющий крайние шарниры A и C данной группы (рисунок 11б).
В результате определяются угол γ и размер AC, после чего в треугольнике ABC становятся известными все три стороны. По теореме косинусов можно определить любой из углов этого треугольника. В данном случае определяется угол α (рисунок 11в), т.к. для дальнейшего решения задачи необходимо знать угол φ2.
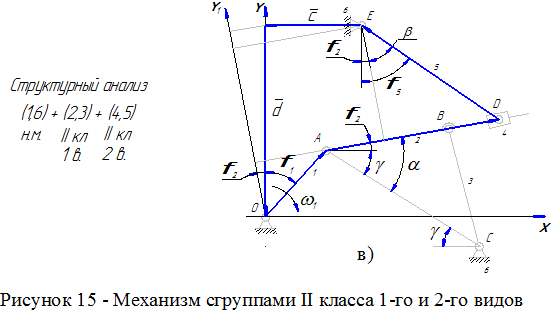
Векторный многоугольник, включающий группу второго класса второго вида, рассматривается в проекции на ось Y1, проведенной перпендикулярно направляющей ABD (рисунок 11в). Полученное алгебраическое уравнение позволяет определить угол β и далее искомый угол φ5.
Конкретно аналитическое определение углового перемещения выходного звена 5, представленного на рисунке 11 механизма (с учетом изложенных выше рекомендаций), будет иметь следующий вид:
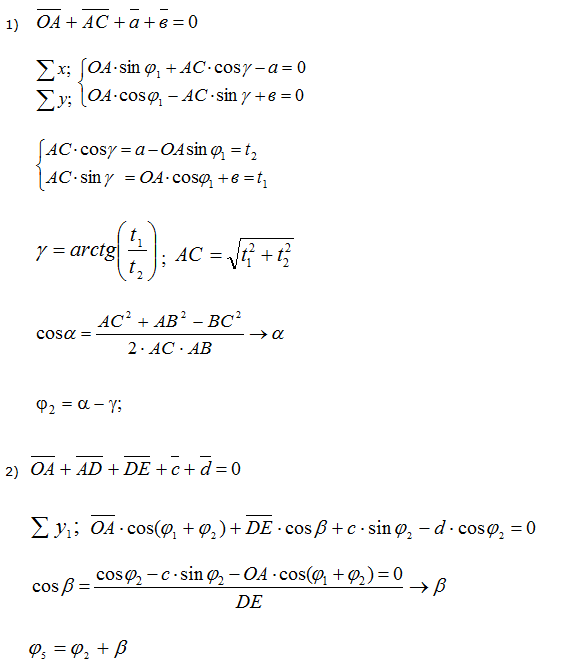
По этим уравнениям с помощью ЭВМ определяется угловое перемещение выходного звена φ5 в рад, угловая скорость ω5 в рад/с, угловое ускорение ε5 в рад/с2 для “n” положений механизма.
Далее: